Stop AI Hallucinations Early: How Meta's DeepConf Uses Token Confidence to Cut Inference Costs by 80%

1 Introduction: Is AI Capable of “Self-Reflection”?

In the current field of Artificial Intelligence, Large Language Models (LLMs) can already write poetry, write code, and even solve complex mathematical problems. But have you ever wondered: when an AI answers a question, is it 100% certain, or is it just “speaking nonsense with a straight face”?

Typically, to make AI solve problems more accurately, we ask it to “think of multiple solutions” (terminologically known as Parallel Thinking or Self-Consistency). This is like a teacher asking you to calculate a math problem 100 times during an exam to see which answer appears the most. While effective, this is extremely wasteful of time and computing power.

The paper introduced today, Deep Think with Confidence (DeepConf), proposed by a research team from Meta AI and UCSD, attempts to solve this problem. They have endowed AI with a capability: Real-time Confidence Perception. If the AI realizes it is becoming “diffident” halfway through a calculation, it stops immediately to avoid wasting time. This not only significantly reduces costs but can even increase the probability of getting the right answer!

• Paper Link: arXiv:2508.15260
• Project Code: GitHub

2 Problem Definition: Why Do We Need “Confident” Thinking?

Before diving into technical details, let’s look at the thorny challenge this paper aims to solve.

2.1 The Dilemma of Parallel Thinking

Imagine you are participating in a difficult math competition.

• Method A (Single Shot): You calculate only once and hand in the paper. It is easy to get it wrong due to a small careless mistake.
• Method B (Parallel Thinking / Majority Vote): You summon 100 clones and let each clone solve the problem independently. Finally, everyone votes, and the answer with the most votes is chosen.

Current state-of-the-art AI reasoning techniques use Method B. Although this significantly improves accuracy, it brings three huge problems:

1. High Cost: Hiring 100 clones to solve problems means paying 100 salaries (computing resources). The paper points out that to improve accuracy by 14%, it might require consuming hundreds of millions of extra tokens, which is almost unacceptable for commercial applications.
2. Diminishing Returns: More clones aren’t always better. Once the number of clones reaches a certain point, accuracy stops improving and may even drop because everyone starts guessing randomly.
3. Blind Voting: This is the most critical point. In traditional majority voting, the answer of a math genius and the answer of someone who knows nothing about math and guesses randomly count as just “one vote” in the ballot box. This is obviously unreasonable! If a large number of low-quality reasoning paths (nonsense) mix in, they can easily drown out the correct answer.

3 Methodology: How Does DeepConf Work?

The core idea of DeepConf is built on a simple observation: When a model talks nonsense, its “tone” usually becomes hesitant. But computers don’t understand tone, so how do we quantify this “hesitation” mathematically?

This starts with the most classic concept in Information Theory—Shannon Entropy.

3.1 Measuring Confidence: Starting from Token Entropy

AI generates text word by word (Token by Token). Whenever a word is generated, the model is actually calculating a “probability table” in its mind.

3.1.1 Shannon Entropy 101

Entropy in information theory is used to measure the “uncertainty” or “chaos” of a system.

The formula is as follows:

Where $P_i(j)$ represents the probability that the model predicts the next word is $j$.

This formula might look abstract, so let’s use two real-life examples to contrast, and you will instantly understand why “Low Entropy = High Confidence”:

• Scenario A: High Confidence (Low Entropy, High Peak) Suppose the model is filling in the blank: “The capital of France is [?]”. The model is very certain, and the probability distribution in its mind might look like this:

  • “Paris”: 99%
  • “London”: 0.5%
  • Others: 0.5%

  At this moment, the probability distribution graph will show a huge Peak. Because most of the probability is concentrated on one option, the uncertainty is extremely low, and the calculated Entropy value will be very close to 0.

  Conclusion: Lower Entropy $\rightarrow$ Sharper Probability Distribution $\rightarrow$ More Confident Model.

• Scenario B: Low Confidence (High Entropy, Flat Distribution) Suppose the model is filling in the blank: “For dinner tonight I want to eat [?]”. The model feels anything is possible and is very hesitant:

  • “Burger”: 10%
  • “Pizza”: 10%
  • “Sushi”: 10%
  • … (Everyone is about the same)

  At this moment, the probability distribution graph will be a Flat line. Probabilities are scattered, uncertainty is high, and the calculated Entropy value will be very large.

  Conclusion: Higher Entropy $\rightarrow$ Flatter Probability Distribution $\rightarrow$ More Hesitant/Less Confident Model.

3.1.2 Practical Choice: Token Confidence ($C_i$)

Although Entropy is the gold standard for measuring confidence, it has a drawback in practical engineering: Calculation is too slow. To calculate exact Entropy, we have to sum up the probabilities of tens of thousands of words in the dictionary.

To pursue extreme speed, the paper designed a substitute metric Token Confidence, which only looks at the top $k$ words with the highest probability (e.g., Top-20):

This metric cleverly uses mathematical transformation:

• When the model is very confident (like Scenario A), the competitors’ probabilities are extremely low (approaching 0). After taking the Log, they become large negative numbers. Taking the average and adding a negative sign results in a large positive number.
• When the model is not confident (like Scenario B), everyone’s probabilities are similar. The Log values won’t be too negative, resulting in a smaller positive number.

3.2 Evaluating the Entire Path: Catching the “Black Sheep”

Having the confidence of a single word is not enough; we need to evaluate the quality of the entire Reasoning Trace.

3.2.1 The Trap of Averages

The most intuitive approach is to calculate the average confidence of the entire text. But this has a fatal flaw: High scores can mask low scores. Imagine a 100-step reasoning process where 95 steps are fluff (high confidence), but only the crucial 5 steps have flawed logic (low confidence). If you take the average, the whole segment still looks like it has a high score, but the answer is wrong.

3.2.2 Solution: Group Confidence

DeepConf introduces the concept of a Sliding Window. Instead of looking at the overall average, it uses a magnifying glass to check confidence segment by segment (e.g., every 1024 Tokens as a group).

This has two benefits:

1. Smoothing: Filters out noise from single words.
2. Capturing Local Collapse: This is the most important part! Once a section of “incoherent speech” or “logic stall” appears in the reasoning process, the Group Confidence for that interval will plummet.

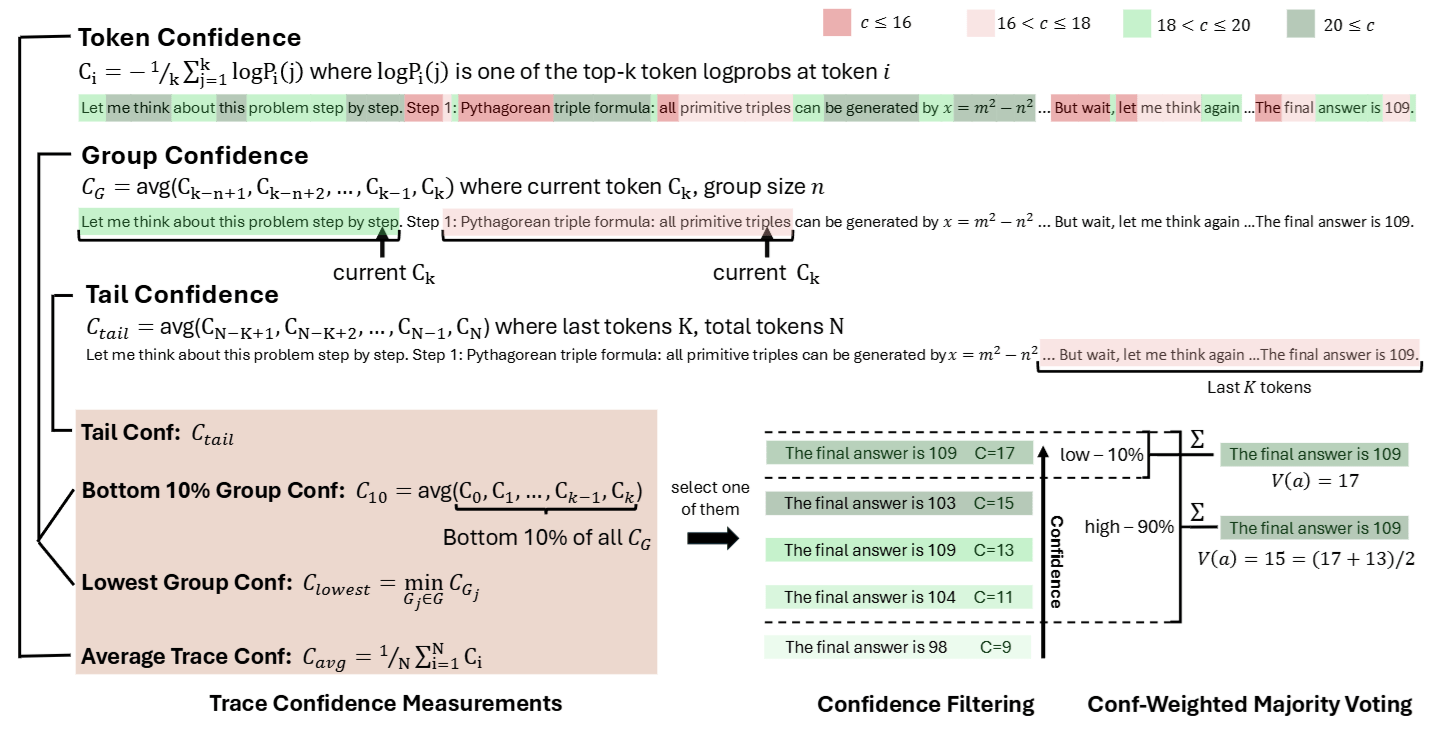
3.3 Three Scoring Strategies

With Group Confidence, how do we give a final score to the entire path? The paper proposes three metrics, applying the Bucket Theory (how much water a bucket can hold depends on its shortest plank):

1. Lowest Group Confidence: Find the segment with the lowest score in the entire path and use it as the grade for this path. As long as one segment of logic collapses, the entire path fails.
2. Bottom 10% Group Confidence: Find the worst performing 10% of segments and average them. This is slightly more robust than just looking at the lowest score, avoiding being misled by a single extreme value.
3. Tail Confidence: Only look at the last segment of the reasoning process. Since reasoning usually gets harder towards the end, if the ending is stable, it usually implies the preceding derivation was decent.

3.4 Key Application Workflows: Offline and Online

Understanding how to score, how exactly is DeepConf applied? The paper proposes two distinct scenarios.

3.4.1 Scenario 1: Offline Thinking (Filtering) — Grading After the Exam

In this scenario, assuming cost is no object, we have already let the model generate 100 complete solution paths. Our task is: Among these 100 paths, how do we choose the most correct answer?

DeepConf performs two layers of optimization here:

Step 1: Confidence Filtering — Separating Wheat from Chaff We no longer let all paths participate in the vote. We first calculate the confidence score for each path (e.g., using Bottom-10%) and then filter. The paper proposes two strategies:

• Elite Strategy (Top 10%): Only keep the 10 paths with the highest scores and throw the remaining 90 into the trash. This approach assumes “truth is held by the few.”
• Mass Strategy (Top 90%): Only remove the bottom 10% “trash” scores and keep most paths. This approach is more robust.

Step 2: Weighted Majority Voting — Expert Voice The remaining paths vote, but it is no longer one person, one vote.

• If a path has high confidence (e.g., 0.9 points) and votes for answer A, answer A gets 0.9 points.
• If a path has low confidence (e.g., 0.2 points) and votes for answer B, answer B only gets 0.2 points. Ultimately, the answer with the highest score wins. This ensures high-quality reasoning dominates the final result.

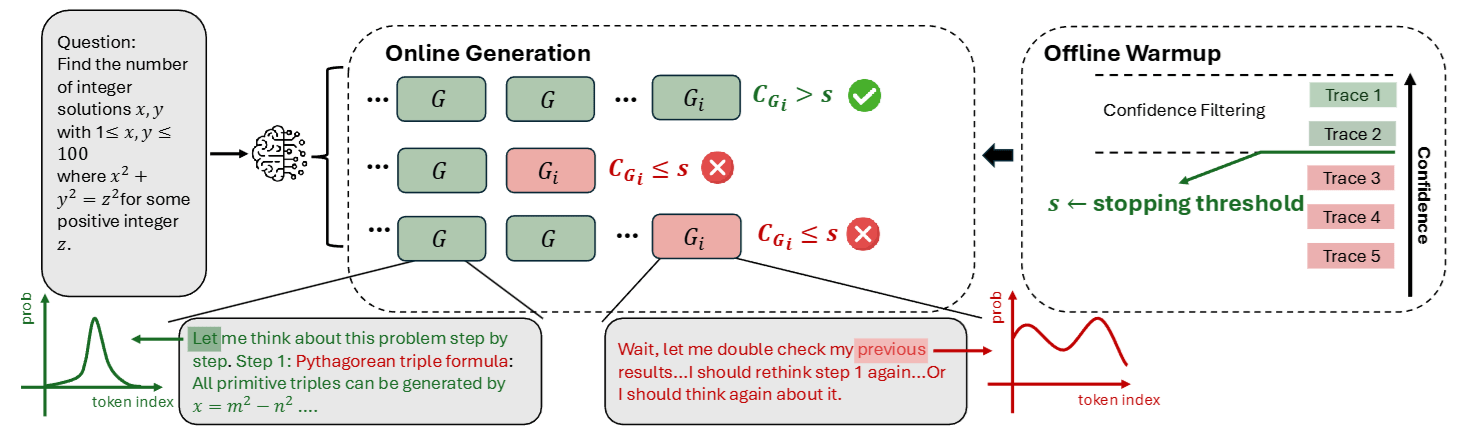
3.4.2 Scenario 2: Online Thinking (Real-time Control) — Teacher Proctoring

This is the most essential part of the paper and the biggest money-saver for companies! In this scenario, we generate and check simultaneously. The goal is: once we discover the student (model) starts writing nonsense, immediately take the paper away (stop generation) and don’t waste time.

This process is slightly more complex, so we break it down into three steps:

Step 1: Offline Warmup — Setting the “Passing Grade” Before officially starting, we let the model generate a small batch of complete paths (e.g., 16 paths).

• We calculate the confidence scores for these 16 paths.
• Suppose we want to maintain a Top 10% standard; we look at what the score is for the top 10% within these 16 paths (e.g., 0.8 points).
• This 0.8 points becomes the Life-or-Death Threshold ($s$) for all subsequent paths.

Step 2: The Kill Switch — Immediate Stop Loss Then, large-scale generation begins. During the generation of each path, the system continuously calculates the current Group Confidence.

• Remember Group Confidence is a sliding window? We calculate the score with every generated word.
• Key Logic: If the score of this small segment now is already lower than the threshold $s$ (e.g., drops to 0.4 points), we can conclude that the Lowest Score of this path will absolutely not be higher than 0.4.
• Action: Since this path is destined to fail, the system immediately cuts off generation (Early Stop).
• Benefit: This path might have originally required writing 1000 words; we killed it at the 200th word, directly saving the computing cost of 800 words!

Step 3: Adaptive Sampling — Quit While You’re Ahead We also need to know “when to stop generating new paths.”

• Every time a valid path is finished, we update the voting result once.
• If we find the vote share for a certain answer has exceeded 95% (high consensus), it means everyone agrees, and the outcome is decided.
• At this point, we stop the entire task and output the answer. There is no need to waste money to reach 100 paths.

4 Experimental Results: Data Speaks

How effective is DeepConf? The paper tested it on high-difficulty datasets like AIME (Math Competition) and GPQA (Graduate-Level Science Q&A), and the results were stunning.

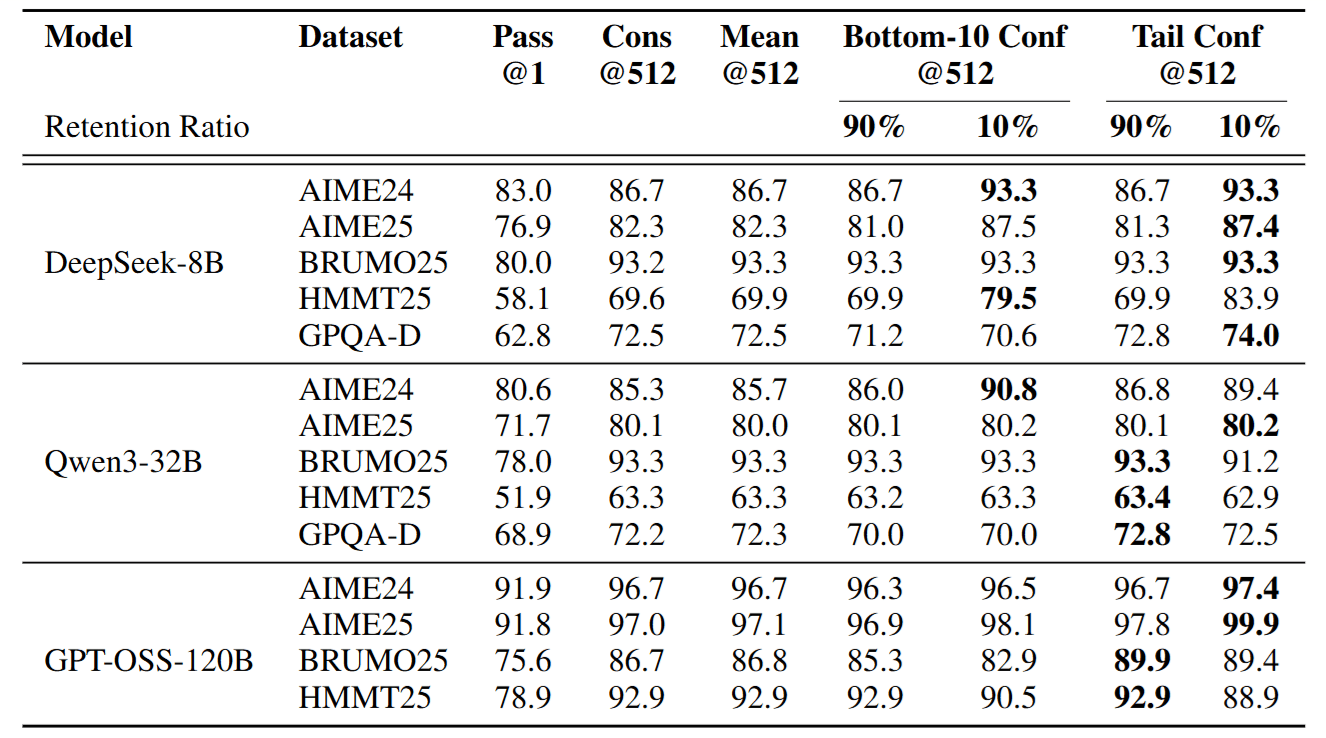
4.1 “Less is More”: Discarding Answers Improves Accuracy

In offline tests, research found that if we discard 90% of low-confidence paths and only let the remaining 10% elite vote, the accuracy is often higher than letting everyone vote.

• For example, DeepSeek-8B on AIME24: Traditional voting accuracy was 86.7%, but after DeepConf filtering, it rose to 93.3%. This proves that low-confidence paths are mostly noise.

4.2 Cost-Saving Miracle: Costs Drop, Performance Stays

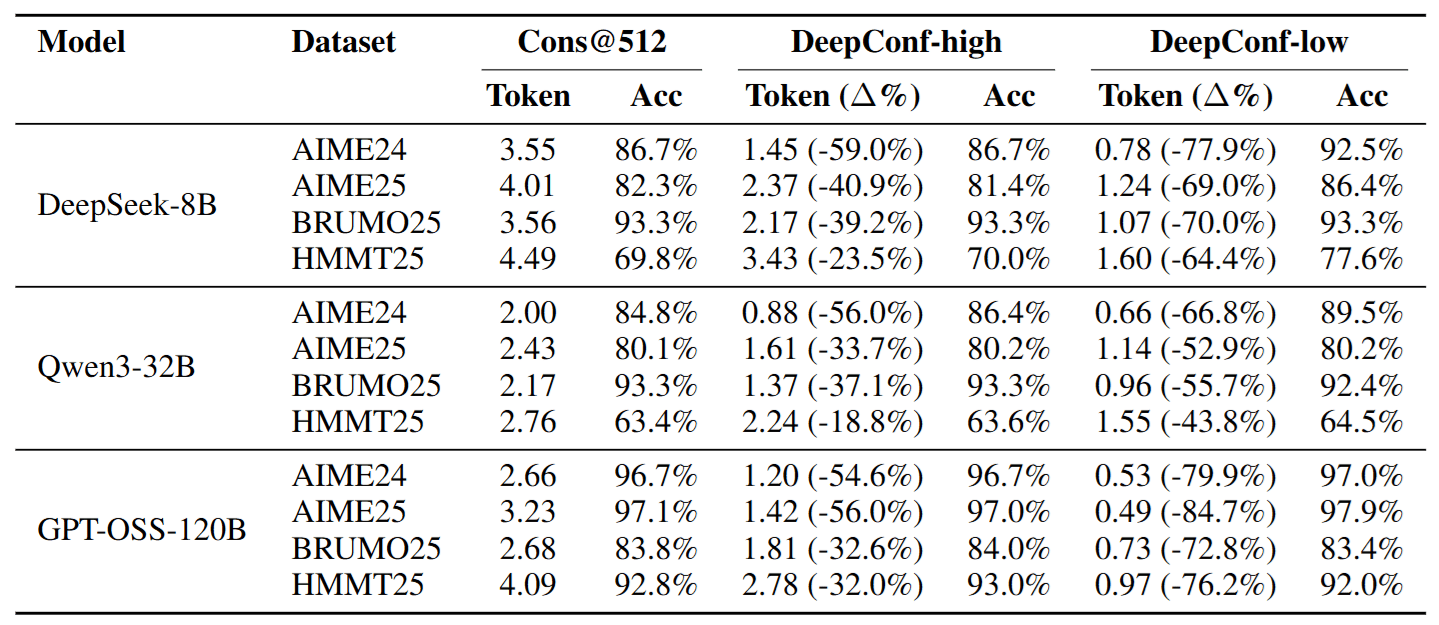
In online tests, DeepConf demonstrated extreme efficiency.

• DeepConf-low (Aggressive Saver): In some tasks, it can save up to 84.7% of Tokens while keeping accuracy flat or even improving it! This means a task that originally took 10 hours to run might now finish in 2 hours.
• DeepConf-high (Conservative Stable): Saves 20%~50% of costs stably with almost no sacrifice in accuracy.

4.3 Local Beats Global

Experimental data also confirmed that using metrics like Bottom-10% or Tail, which focus on “local” and “weakest link” aspects, discriminate quality better than simply looking at the overall average. This verifies the hypothesis that “a wrong reasoning chain often stems from the collapse of a specific segment.”

5 Conclusion: Teaching AI to “Know When to Stop”

Deep Think with Confidence (DeepConf) is not about training a more powerful new model, but teaching us how to use existing models smarter.

Through a simple confidence monitoring mechanism, DeepConf successfully solves the high cost problem of Parallel Thinking. It tells us:

1. AI has “self-awareness”; it knows when it is making things up.
2. Instead of letting AI blindly generate massive amounts of text, it is better to call a halt immediately when it hesitates.
3. This process of “separating the wheat from the chaff” not only saves huge computing costs but often makes the final answer more precise.

For future AI application developers, this paper provides an extremely valuable insight: High-quality reasoning lies not in thinking more, but in thinking “precisely” and “stably”.