ACL 2025 | 超越 Self-Consistency！CER 論文解析：無需訓練，靠「過程自信度」激發 Llama 3 與 DeepSeek 推理潛能

2026-01-03 約 5184 字預計閱讀 23 分鐘

深入解析 ACL 2025 重磅論文 CER (Confidence Enhanced Reasoning)，這項無需訓練 (Training-free) 的技術透過分析「推理過程自信度」並過濾 Logits 雜訊，顯著提升 Llama 3 與 DeepSeek-R1 的數學及問答準確率。了解 CER 如何克服 Self-Consistency 的缺陷，成為優化 LLM 推理能力的最佳輕量化方案。

1 前言

在大型語言模型 (LLMs) 的推理任務中，我們經常發現模型雖然能給出答案，但我們很難判斷這個答案是否「可靠」。目前學界最主流的做法是 Self-Consistency (SC)，也就是讓模型多生成幾次，然後用「多數決」選出答案。然而，這種方法有一個致命傷: 它假設每一條推理路徑的權重都是平等的，忽略了模型在生成過程中的「猶豫」或「自信」。

這篇文章要探討的論文 CER (Confidence Enhanced Reasoning)，提出了一個優雅且無需微調 (Training-free) 的解決方案。這篇論文已被 ACL 2025 Main Conference 接收，其核心貢獻在於證明了 「推理過程中的自信度 (Process Confidence) 」比單純看「最終答案的自信度」更具參考價值。

在開始深入細節之前，我們先列出本篇論文的相關資源:

論文連結: arXiv:2502.14634
程式碼: GitHub Repository

這篇論文的核心價值

CER 的最大亮點在於它的輕量化與通用性。它不需要訓練額外的獎勵模型 (Reward Model) ，也不需要微調 LLM。它僅僅透過精心設計的 Prompt 配合模型輸出的 Logits (機率分佈) ，就能顯著提升現有模型 (包含 Llama 3, Mistral, 甚至 DeepSeek-R1) 在數學與開放域問答上的準確率。這對於資源受限、無法自行訓練模型的我們來說，是一個極具實戰價值的技術。

2 問題定義

在深入了解 CER 的具體解法之前，我們必須先釐清: 為什麼現有的 LLM 推理增強方法還不夠好？

隨著大型語言模型的能力越來越強，我們開始讓它們處理需要多步驟思考的複雜任務 (如數學證明、Multi-Hop 知識問答) 。然而，LLM 本質上是一個機率模型，這意味著它們天生就伴隨著「不確定性」與「幻覺 (Hallucination) 」。為了緩解這個問題，學界發展出了許多技術，但它們各自都有明顯的痛點。

我們將本篇論文試圖解決的挑戰歸納為以下三點:

2.1 Limitations of Self-Consistency

目前提升推理能力最主流的方法是 Self-Consistency (SC)。它的概念很簡單: 讓模型對同一個問題生成 $K$ 條不同的推理路徑 (Reasoning Paths) ，然後統計出現次數最多的答案作為最終結果 (Majority Voting) 。

這種方法雖然有效，但隱含了一個危險的假設: 每一條生成的路徑都是「平等」的。

在現實情況中，這並不合理。

情境 A: 模型經過嚴謹推導，非常有信心地得出答案。
情境 B: 模型在推導過程中充滿猶豫 (低機率) ，最後剛好湊出一個答案。

在 SC 的機制下，情境 A 和情境 B 的這一票權重是一樣的。更糟糕的是，當模型出現「一致性幻覺 (Consistent Hallucination) 」時——即模型很有信心地、反覆地生成同一個錯誤答案——SC 會毫不猶豫地選出這個錯誤答案，因為它只看「數量」，不看「品質」。

2.2 Noise in Whole-Sequence Uncertainty

既然單純數票數有問題，那我們引入「自信度 (Confidence) 」來加權不就好了嗎？通常我們可以用模型輸出的 Logits 來計算一句話的機率或熵 (Entropy) 。然而，直接計算整條推理路徑 (Whole-sequence) 的自信度會有很大的雜訊。

一個典型的思維鏈 (Chain-of-Thought, CoT) 包含了大量的功能性詞彙 (Functional Words) ，例如:

“First, we need to calculate…”
“Therefore, the answer is…”
“Based on the assumption…”

這些詞彙對於文法通順很重要，模型生成它們的機率通常非常高 (自信度高) 。如果我們計算整段文字的平均機率，這些無關緊要的高分 Token 會稀釋掉真正關鍵的資訊 (例如某個關鍵的運算數字或實體名稱) 。這導致我們很難區分一條「邏輯正確的路徑」和一條「廢話連篇但文法通順的路徑」。

訊號與雜訊

我們可以把這個問題想像成「訊噪比 (Signal-to-Noise Ratio) 」的問題。在推理過程中，數值和專有名詞是真正的「訊號」，而連接詞和填充詞則是背景「雜訊」。如果我們把整段話混在一起算平均，強大的背景雜訊會掩蓋掉微弱但關鍵的訊號波動。

2.3 Neglect of Intermediate Reasoning Steps

複雜推理往往是「一環扣一環」的。一個數學題可能需要五個步驟，如果第二步算錯了，即便後面三步的推導邏輯再完美、模型再有自信，最終答案也是錯的。

現有的許多方法傾向於只評估最終生成答案的自信度。這忽略了一個核心事實: 錯誤往往發生在中間。

本篇論文認為，要判斷一條路徑是否可靠，我們不能只看終點，必須檢查過程中的每一個轉折點。如果模型在中間某一步驟表現出猶豫 (高熵值、低機率) ，這就是一個強烈的警訊，暗示這條路徑的權重應該被大幅降低。

3 方法介紹

CER (Confidence Enhanced Reasoning) 的核心理念在於:

不要看整句話，只看重點；不要只數人頭，要看信心。

這是一個完全 無需訓練 (Training-free) 的框架，不需要修改模型的權重，也不需要外部的 Reward Model。它純粹利用現有 LLM 在推理時輸出的 Logits (機率分佈) 來進行精細的後處理。

我們可以將 CER 的運作流程拆解為四個嚴謹的步驟，這四個步驟環環相扣，將非結構化的自然語言轉化為可計算的數學分數。

3.1 Reasoning Path Generation

首先，我們需要讓模型對同一個問題生成多種可能的解法。這一步與 Self-Consistency 類似，我們通常會設定較高的採樣溫度 (例如 $T=0.7$ 或 $T=1.0$ ) ，讓模型發揮創造力，生成 $K$ 條不同的推理路徑 (Reasoning Paths) 。

但在這裡，CER 做了一個關鍵的改動: Prompt 的設計。

為了後續能讓程式自動抓取重點，我們必須跟模型「約法三章」。透過精心設計的 Prompt (如下圖所示) ，我們要求模型在每一個推理步驟結束時，必須依照特定的格式輸出中間答案。

CER 用於數學推理的 Prompt 範例。注意它要求模型使用 ‘Answer: [answer]’ 格式輸出。

數學任務: 要求輸出 Answer: [數值]。
問答任務: 要求輸出 Response: [實體/短語]。

這樣做的目的是將非結構化的思維鏈 (CoT) 轉化為「半結構化」的數據，讓我們後續可以用正規表達式 (Regex) 輕鬆提取資訊。

3.2 Identifying Critical Tokens

這是 CER 與傳統方法的分水嶺。傳統方法會計算整句生成的 Log-Likelihood，但 CER 認為: 一句話中大部分的詞都是雜訊 (填充詞) ，只有推理的結點 (Node) 才是訊號。

在實作上，我們利用 Regex 抓取 Prompt 中定義好的標籤 (如 Answer: 或 Response:) ，並鎖定其後的內容作為「關鍵字」。

數學任務 (Math Tasks): 關注 數值 (Numerical values)。例如在計算過程中出現的 “100”, “5”, “125”。
開放域問答 (Open-Domain QA): 關注 專有名詞 (Proper Nouns)。例如人名、地名或特定實體。

透過這個篩選機制，我們排除了 “Therefore”, “We calculate”, “is equal to” 這些高機率但無資訊量的詞彙，確保我們的自信度分數純粹反映了模型對「推理結果」的把握。

3.3 Confidence Estimation

一旦鎖定了關鍵字，我們就需要計算分數。這分為兩個層次: 單詞層級與路徑層級。

3.3.1 單詞層級聚合 ( $f$ ): 從 Token 到 Word

一個關鍵字 (例如 “125”) 可能由多個 Token 組成 (例如 Token IDs [1, 2, 5]) 。我們需要一個函數 $f$ 來計算這個單詞的整體自信度 $c_w$ 。

論文驗證後發現，最有效的方法是計算 聯合機率 (Joint Probability)，也就是將所有組成 Token 的機率相乘:

c_w = f(\{p_t | t \in w\}) = \prod_{t \in w} p_t

工程實作細節: 避免數值下溢 (Underflow)

直接將多個小數 (機率) 相乘，在電腦中可能會因為數值過小而發生 Underflow (變成 0) 。雖然關鍵字通常很短，風險較低，但在嚴謹的程式實作中，我們通常會採用 Log-Sum-Exp 的技巧:

c_w = \exp\left( \sum_{t \in w} \log(p_t) \right)

我們先把機率取 Log 變成負數相加 (這在數值上非常穩定) ，最後再用 Exponential 還原回 [0, 1] 的機率空間。這在數學上是等價的，但在工程上更安全。

3.3.2 路徑層級聚合 ( $g$ ): 從 Word 到 Path

一條推理路徑包含多個步驟，每個步驟都有一個中間答案。我们需要一個函數 $g$ 將這些中間分數綜合成整條路徑的分數 $C_{path}$ 。

CER 採用的是 線性加權平均 (Linearly Weighted Mean)。

C_{path} = \frac{\sum_{j=1}^{n} j \cdot c_{a_j}}{\sum_{j=1}^{n} j}

其中 $j$ 是步驟的序號 (Step 1, Step 2…) ， $c_{a_j}$ 是第 $j$ 步關鍵答案的自信度。

為什麼要加權？ 因為推理是累積的。Step 1 通常只是理解題目，較為簡單；而最後的 Step $N$ 往往依賴於前面所有步驟的正確性。如果模型對最後一步非常有信心，通常暗示前面的基礎也是穩固的。因此，越靠近最終答案的步驟，權重越重。

3.4 Confidence-Weighted Aggregation

最後一步是從 $K$ 條路徑中選出最終答案。

Self-Consistency (Baseline): 單純計算每個答案出現了幾次 (Count Voting) 。
CER (Our Method): 計算支持該答案的所有路徑的自信度總和。

Score(Answer) = \sum_{y \in \text{Paths leading to Answer}} C_{path}(y)

我們最終選取得分 $Score(Answer)$ 最高的那個答案。

透過這種方式，如果有一條路徑雖然得出了某個答案，但中間過程猶豫不決 (自信度低) ，它對總分的貢獻就會很小；反之，一條邏輯清晰、每一步都很有把握的路徑，將會對最終決策產生決定性的影響。

4 實驗結果

在科學研究中，實驗數據不僅僅是證明「分數變高了」，更重要的是驗證我們最初的假設是否成立。本篇論文進行了廣泛的實驗，涵蓋了不同的模型規模 (從 3B 到 8B) 以及不同性質的任務 (數學推理與開放域問答) 。

我們將實驗結果歸納為以下幾個值得注意的重點:

4.1 整體效能: CER 全面優於 Baseline

作者在三個數學資料集 (GSM8K, MATH, MathQA) 和兩個問答資料集 (TriviaQA, HotPotQA) 上進行了測試。比較的基準 (Baseline) 包含貪婪解碼 (Greedy) 、Self-Consistency (SC) 以及其他基於機率的統計方法。

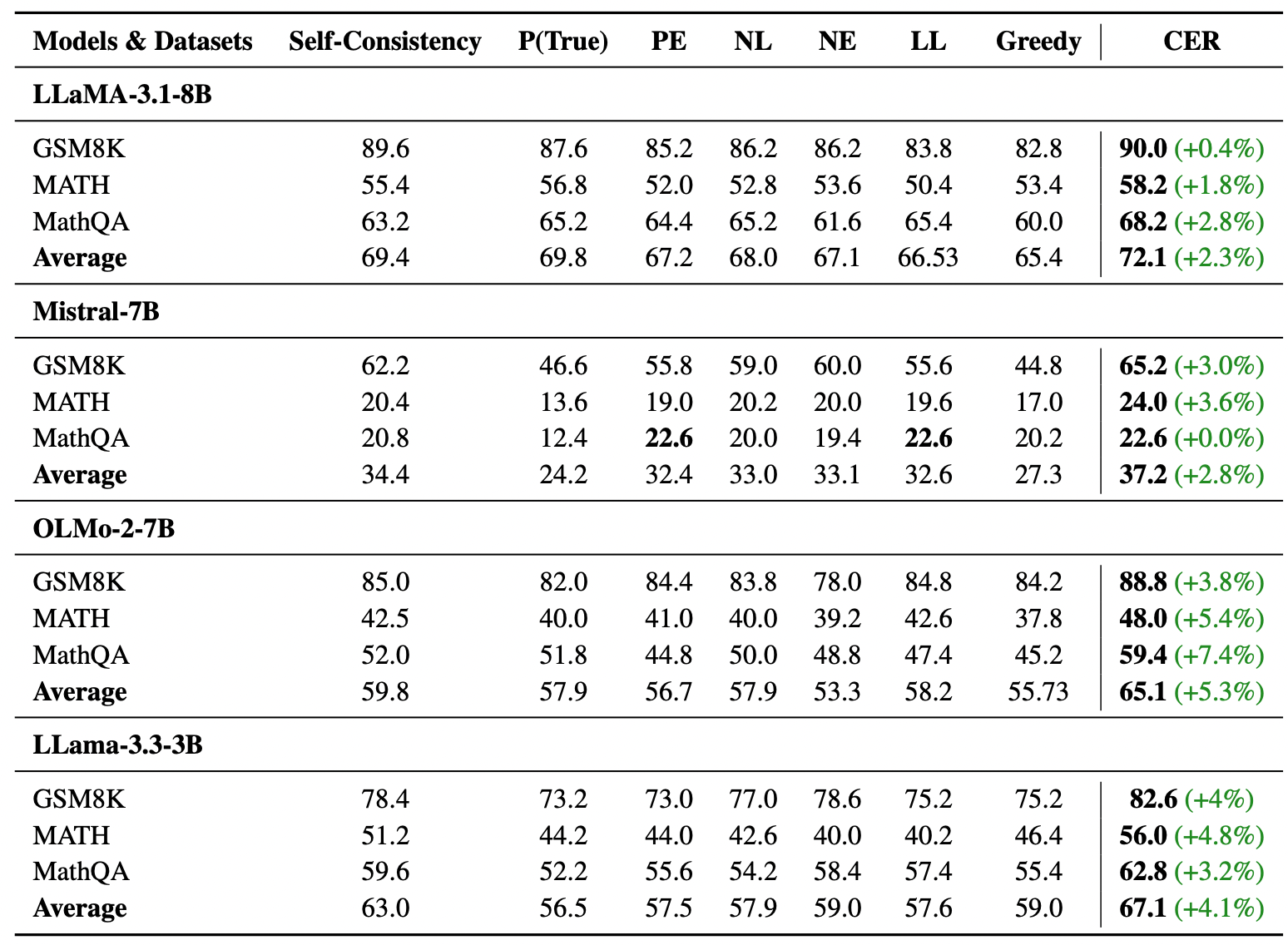
Table 1: 在數學任務上的準確率比較。綠色數字代表相較於最佳 Baseline 的提升幅度。

從表格中我們可以觀察到:

一致性提升: CER 在所有資料集和模型上都取得了比 Baseline 更好的成績。
顯著差異: 在 MathQA 這種難度較高的資料集上，提升幅度甚至達到了 7.4% (OLMo-2-7B) 。

4.2 「弱模型」與「難任務」獲益更多

這是一個非常有趣的發現。如果我們仔細觀察數據，會發現提升的幅度並不是均勻的。

強模型 (Strong Models): 對於像 Llama 3.1 8B 這樣強大的模型，在相對簡單的 GSM8K 任務上，提升幅度較小 (約 0.4%) 。這是因為強模型原本就很有信心，且錯誤率極低，改進空間有限。
弱模型 (Weak Models): 對於參數較少或推理能力較弱的模型 (如 OLMo 2 7B 或 Mistral 7B) ，CER 帶來的提升非常巨大。

為什麼弱模型進步更多？

這驗證了 CER 的篩選能力。弱模型在面對難題時，往往會生成許多「似是而非」的推理路徑 (雜訊) 。CER 就像一個過濾器，透過檢查中間步驟的自信度，成功幫弱模型篩掉了那些它自己都「心虛」的錯誤路徑，從而大幅提升了最終答案的可靠性。這對於我們想在邊緣裝置上部署小型模型 (SLM) 極具啟發意義。

4.3 核心假設驗證: 「過程」真的比「結果」重要

這是整篇論文在科學上最重要的一個實驗 (Ablation Study) 。為了證明「檢查中間步驟」是必要的，作者設計了一個對照組 CER-LAST，即忽略中間過程，只計算「最後一個答案」的自信度。

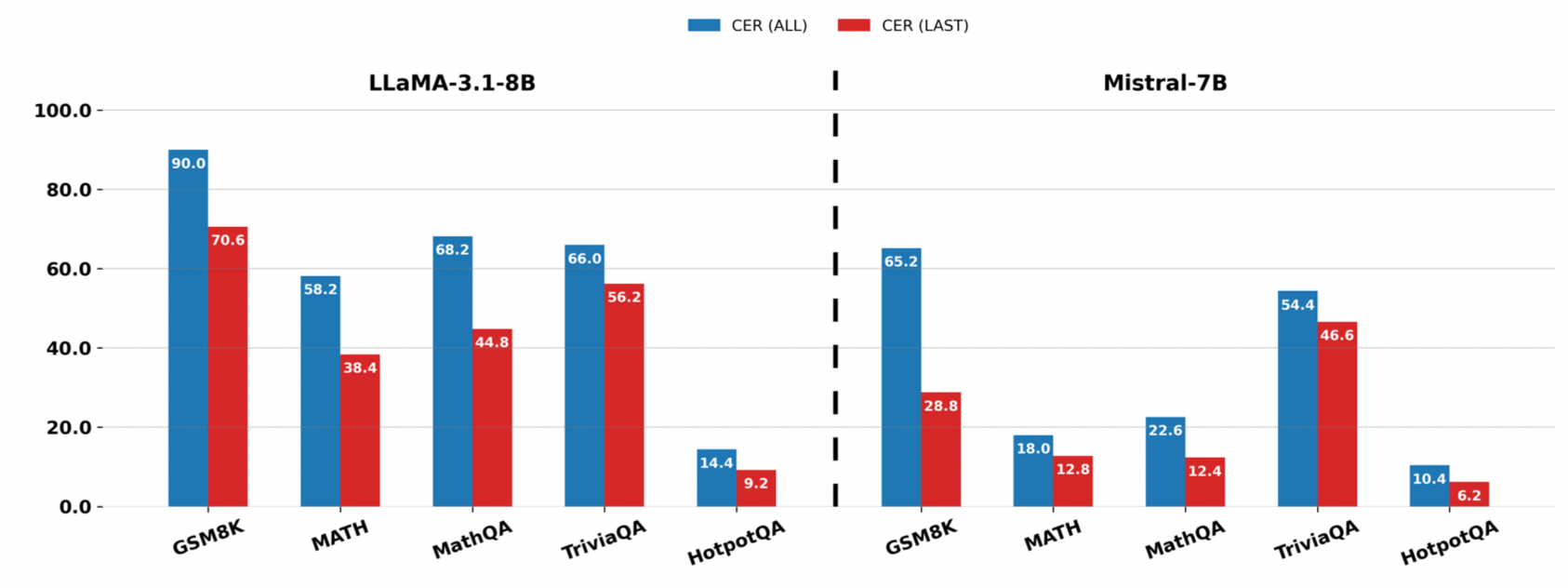
Figure 3: CER (藍色，考慮所有步驟) 與 CER-LAST (紅色，只看最後一步) 的效能比較。

結果如上圖所示，CER (Blue Bar) 在所有情況下都顯著優於 CER-LAST (Red Bar)。

這直接證明了作者的核心論點: 模型可能在最後給出一個很有自信的錯誤答案 (Overconfidence) ，但在中間推理過程中其實已經顯露出了猶豫。如果我們只看最後一步，就會被模型騙過；只有全程監控，才能抓出這些隱藏的錯誤。

4.4 數學 vs. 知識問答: 推理與記憶的差異

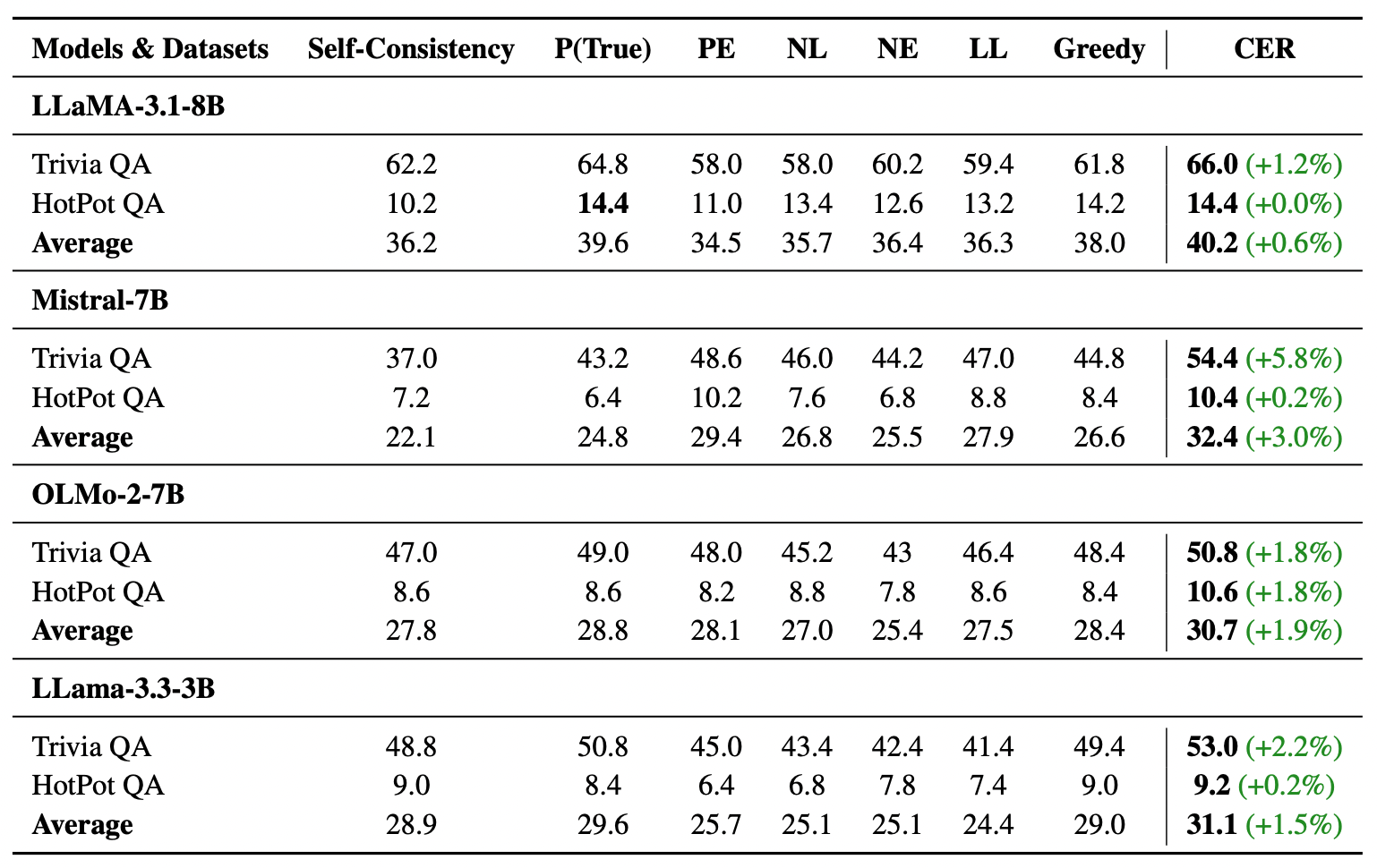
Table 2: 在開放域問答任務（TriviaQA, HotPotQA）上的準確率比較。可以看到部分模型（如 Llama-3.2-3B）在知識密集型任務上的提升幅度不如數學任務顯著。

比較數學任務與開放域問答 (QA) 的結果，我們發現 CER 在數學上的表現通常比 QA 更穩定。

特別是 Llama 3.2 3B 這個模型，在數學上提升了 4.1%，但在 QA 上幾乎沒有幫助。這揭示了 CER 的邊界:

數學是邏輯推理: CER 可以透過自信度判斷邏輯是否連貫。
QA 是知識檢索: 如果模型參數裡根本沒有這個知識 (Knowledge Gap) ，不管怎麼推理、自信度怎麼算，模型都不可能答對 (這被稱為「因無知而產生的幻覺」) 。

這告訴我們: CER 是用來增強「推理能力」的，而不是用來彌補「知識庫存」的。

4.5 適用於最新的推理模型 (DeepSeek-R1)

Table 3: CER 應用於 DeepSeek-R1-Distill-Qwen-7B 模型上的表現。即使在經過強化學習優化（RL）的強推理模型上，CER 依然能將 GSM8K 的準確率進一步推升。

為了驗證方法的通用性，作者還測試了近期非常熱門的 DeepSeek-R1 變體 (經過強化學習優化的推理模型) 。結果顯示，即使是這種已經專門針對 CoT 微調過的模型，CER 依然能將 GSM8K 的準確率從 87.2% 提升到 90.2%。

這意味著 CER 所捕捉到的「自信度訊號」，是模型內部普遍存在的特徵，即便是經過 RLHF 訓練後的模型也依然保有這些資訊可供利用。

5 結語

恭喜我們一起完成了這篇論文的深度研讀！回顧 CER (Confidence Enhanced Reasoning) 的整套架構，我們可以發現它雖然技術實作上不複雜，但其背後的洞察力 (Insight) 卻非常深刻。

這篇論文給了我們一個重要的啟示: 在大型語言模型的推理中，「過程」的品質決定了「結果」的可靠性。

過去的 Self-Consistency (SC) 方法雖然透過「多數決」解決了隨機性的問題，但它忽略了模型內部的細微聲音——那些隱藏在 Logits 中的猶豫與自信。CER 透過一個簡單而優雅的假設——「只看關鍵步驟，忽略填充雜訊」，成功地證明了我們不需要昂貴的額外訓練，只需要聰明地解讀模型已經給出的訊號，就能大幅提升推理的準確度。

Final Takeaway

CER 教會了我們兩件在工程實戰中極具價值的事:

資料結構化的力量: 透過 Prompt 強制模型輸出 Answer: 或 Response: 標籤，我們能將非結構化的自然語言轉化為半結構化的資料。這是在不改變模型架構下，提升系統可控性的關鍵技巧。
Logits 是被低估的金礦: 模型的原始輸出 (Logits) 包含了比最終文字 (Text) 豐富得多的資訊。學會如何去雜存菁 (只算關鍵 Token 的機率) ，是我們從現有模型中榨出更多效能的有效途徑。

最後，雖然 CER 在數學推理上表現亮眼，但實驗也顯示了它在純知識檢索任務上的局限性。這提醒我們，自信度可以過濾「邏輯謬誤」，但無法憑空創造「缺失的知識」。

目錄

目錄

ACL 2025 | 超越 Self-Consistency！CER 論文解析：無需訓練，靠「過程自信度」激發 Llama 3 與 DeepSeek 推理潛能

1 前言