拒絕 AI 一本正經胡說八道!DeepConf 論文解析:如何利用「信心分數」優化推理並大幅節省 Token?

1 前言: AI 懂得「自我反思」嗎?
在現今的人工智慧領域,大型語言模型 (LLM)已經能寫詩、寫程式,甚至解開複雜的數學題。但你有沒有想過,當 AI 在回答問題時,它到底是有十足的把握,還是在「一本正經地胡說八道」?
通常,為了讓 AI 解題更準確,我們會讓它「多想幾種解法」(這在術語上稱為 Parallel Thinking 或 Self-Consistency)。這就像是考試時,老師叫你把題目算 100 遍,然後看哪個答案出現最多次。這雖然有效,但非常浪費時間與算力。
今天要介紹的這篇論文 Deep Think with Confidence (DeepConf),由 Meta AI 與 UCSD 的研究團隊提出,他們試圖解決這個問題。他們賦予了 AI 一種能力: 即時感知自己的信心。如果 AI 發現自己算到一半開始「心虛」了,它就會立刻停下來,不再浪費時間。這不僅大幅節省了成本,甚至還能提高答對的機率!
- 論文連結: arXiv:2508.15260
- 專案程式碼: GitHub
2 問題定義: 為什麼我們需要「有信心」的思考?
在深入技術細節前,我們先來看看這篇論文想要解決什麼棘手的挑戰。
2.1 平行思維 (Parallel Thinking) 的困境
想像你正在參加一場困難的數學競賽。
- 方法 A (單次思考): 你只算一次就交卷。這很容易因為一個小粗心就錯了。
- 方法 B (平行思維 / 多數決): 你召集了 100 個分身,讓每個分身獨立解題。最後大家投票,哪個答案票數多就選哪個。
目前最先進的 AI 推理技術,用的就是 方法 B。這雖然能顯著提升準確率,但卻帶來了三個巨大的問題:
- 成本極高 (High Cost): 請 100 個分身解題,你需要付 100 份的薪水 (計算資源)。論文指出,為了讓準確率提升 14%,可能需要額外消耗上億個 Token 的運算量,這在商業應用上幾乎是不可接受的。
- 效益遞減 (Diminishing Returns): 並不是分身越多越好。當分身數量多到一定程度,準確率就不再提升了,甚至可能因為大家都在亂猜而下降。
- 盲目的民主 (Blind Voting): 這是最關鍵的一點。在傳統的多數決中,一位數學天才的答案和一個完全不懂數學的人亂猜的答案,在投票箱裡都只算「一票」。這顯然不合理!如果有大量低品質的思考路徑 (胡說八道) 混進來,很容易淹沒正確答案。
3 方法介紹: DeepConf 如何運作?
DeepConf 的核心思想建立在一個簡單的觀察上: 當模型在胡說八道時,它的「語氣」通常會變得猶豫不決。 但電腦不懂語氣,我們如何用數學來量化這種「猶豫」呢?
這就要從資訊理論中最經典的概念 —— Shannon Entropy 說起。
3.1 測量信心: 從 Token Entropy 開始
AI 生成文字是一字一字(Token by Token)吐出來的。在每一個字生成時,模型其實都在心裡計算一張「機率表」。
3.1.1 Shannon Entropy 基礎教室
Entropy (熵) 在資訊理論中,是用來衡量一個系統的「不確定性」或「混亂程度」。
其公式如下:
其中 代表模型預測下一個字是 的機率。
這個公式可能看起來很抽象,讓我們用兩個生活化的例子來對比,你就能瞬間理解為什麼「低 Entropy = 高信心」:
情境 A: 高信心 (Low Entropy, High Peak) 假設模型正在填空: 「法國的首都是 [?]」。 模型非常有把握,它腦中的機率分佈可能長這樣:
- “Paris”: 99%
- “London”: 0.5%
- 其他: 0.5%
這時候,機率分佈圖會出現一個巨大的尖峰 (Peak)。因為大部分機率都集中在一個選項上,不確定性極低,算出來的 Entropy 數值會非常接近 0。
結論: Entropy 越低 機率分佈越尖銳 模型越有信心。
情境 B: 低信心(High Entropy, Flat Distribution) 假設模型正在填空: 「今天晚餐我想吃 [?]」。 模型覺得什麼都有可能,很猶豫:
- “漢堡”: 10%
- “披薩”: 10%
- “壽司”: 10%
- … (大家都差不多)
這時候,機率分佈圖會是一條平坦的線 (Flat)。機率分散,不確定性很高,算出來的 Entropy 數值會很大。
結論: Entropy 越高 機率分佈越平坦 模型越猶豫/沒信心。
3.1.2 實戰選擇: Token Confidence ()
雖然 Entropy 是衡量信心的黃金標準,但在實際工程上它有個缺點: 計算太慢。要算出精確的 Entropy,我們得把字典裡幾萬個字的機率全部加總。
為了追求極致的速度,論文設計了一個替代指標 Token Confidence,只看機率最高的 個字 (例如 Top-20):
這個指標巧妙地利用了數學轉換:
- 當模型很有信心時 (像情境 A),競爭對手的機率極低 (趨近於 0),取 Log 後會變成很大的負數,再取平均並加負號,會得到一個很大的正數。
- 當模型沒信心時 (像情境 B),大家機率都差不多,Log 值不會太負,最後得到一個較小的正數。
3.2 評估整條路徑: 抓出「害群之馬」
有了單個字的信心還不夠,我們要評估整串推理過程 (Reasoning Trace) 的好壞。
3.2.1 平均值 (Average) 的陷阱
最直觀的做法是算整段話的平均信心。但这有個致命傷: 高分會掩蓋低分。 想像一段 100 步的推理,其中 95 步都是廢話 (信心很高),只有關鍵的 5 步邏輯錯了 (信心很低)。如果取平均,整段看起來還是高分,但答案卻是錯的。
3.2.2 解決方案: Group Confidence (分組信心)
DeepConf 引入了 滑動視窗 (Sliding Window) 的概念。它不是看整體的平均,而是拿著放大鏡,一段一段地(例如每 1024 個 Token 一組)檢查信心。
這樣做有兩個好處:
- 平滑化: 過濾掉單個字的雜訊。
- 捕捉局部崩潰: 這最重要!一旦推理過程中出現一段「語無倫次」或「邏輯卡頓」,那一個區間的 Group Confidence 就會驟降。
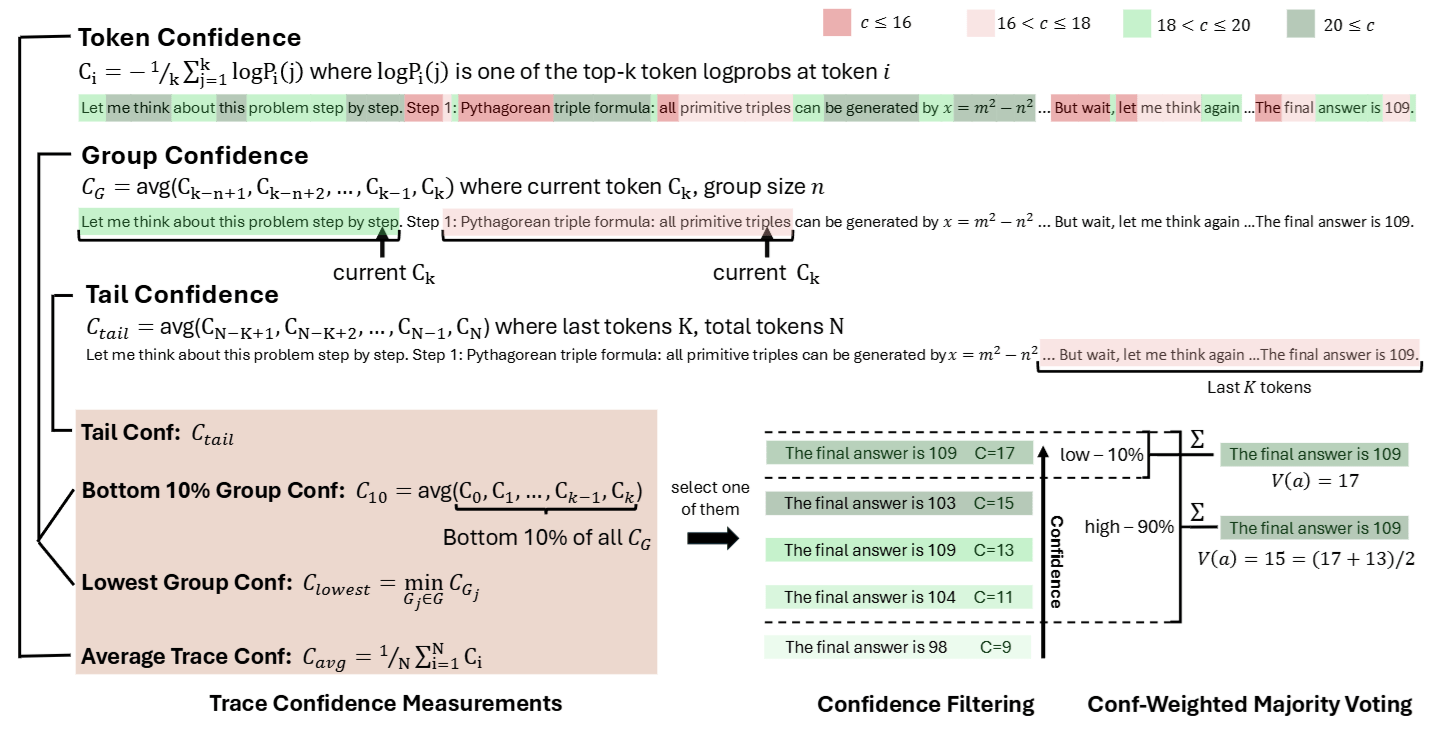
3.3 三種評分策略
有了 Group Confidence,我們如何給整條路徑打最終分數? 論文提出了三個指標,運用了木桶理論 (水桶能裝多少水,取決於最短的那塊木板):
- Lowest Group Confidence (最低分組信心): 找出整條路徑中分數最低的那一段,當作這條路徑的成績。只要有一段邏輯崩潰,整條路徑就不及格。
- Bottom 10% Group Confidence: 找出表現最差的 10% 片段取平均。這比只看最低分更穩健一點,避免被單一極端值誤導。
- Tail Confidence (結尾信心): 只看推理過程的最後一段。因為推理通常越後面越難,如果結尾很穩,通常代表前面推導得不錯。
3.4 關鍵應用流程: Offline 與 Online
了解了如何打分數後,DeepConf 究竟是如何應用的?論文提出了兩種截然不同的場景。
3.4.1 場景一: Offline Thinking (離線篩選) —— 考完試再改卷
在這個場景下,假設我們不計成本,已經讓模型生成了 100 條完整的解答路徑。我們的任務是: 在這 100 條路徑中,怎麼選出最正確的答案?
DeepConf 在這裡做了兩層優化:
Step 1: 信心過濾 (Confidence Filtering) —— 去蕪存菁 我們不再讓所有路徑都參與投票。我們先計算每條路徑的信心分數 (例如用 Bottom-10%),然後進行篩選。論文提出了兩種策略:
- 菁英策略 (Top 10%): 只留下分數最高的 10 條路徑,把剩下 90 條丟進垃圾桶。這種做法假設「真理掌握在少數人手中」。
- 大眾策略 (Top 90%): 只剔除分數最低的 10%「垃圾」,保留大部分路徑。這種做法比較穩健。
Step 2: 加權投票 (Weighted Majority Voting) —— 專家話語權 剩下的路徑進行投票時,不再是一人一票。
- 如果一條路徑信心很高(例如 0.9 分),它投給答案 A,那答案 A 就得 0.9 分。
- 如果一條路徑信心很低(例如 0.2 分),它投給答案 B,那答案 B 只得 0.2 分。 最終,得分最高的答案勝出。這確保了高品質的推理能主導最終結果。
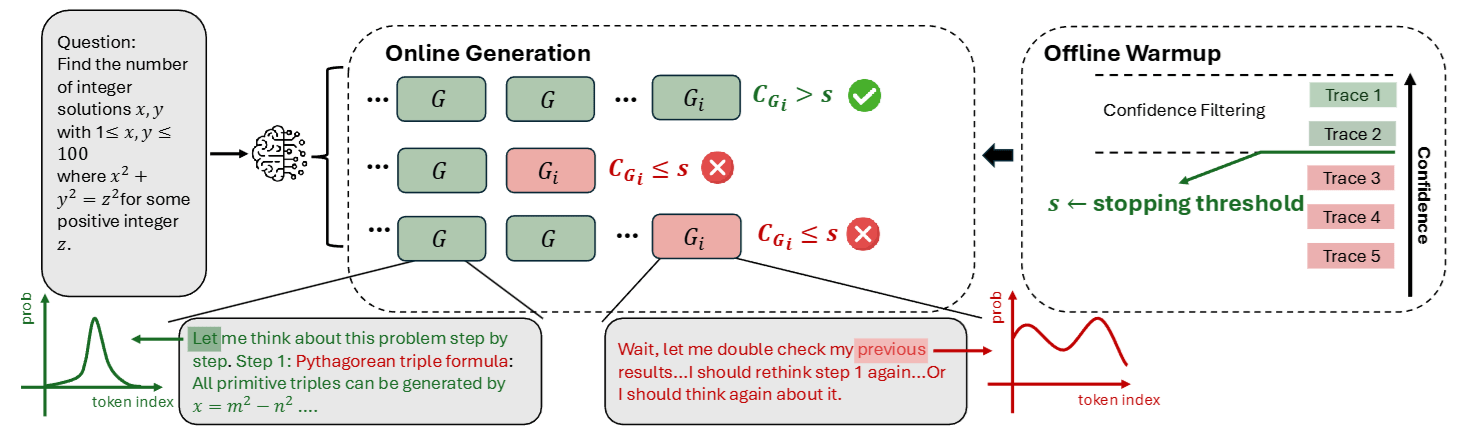
3.4.2 場景二: Online Thinking (線上即時控制) —— 老師監考中
這是這篇論文最精華、最能幫公司省錢的部分! 在這個場景下,我們一邊生成,一邊檢查。目標是: 一旦發現學生 (模型) 開始亂寫,馬上把考卷收走 (停止生成),不要浪費時間。
這個流程稍微複雜一點,我們把它拆解成三個步驟:
Step 1: 熱身 (Offline Warmup) —— 設定「及格線」 在正式開始前,我們先讓模型生成一小批完整的路徑 (例如 16 條)。
- 我們計算這 16 條路徑的信心分數。
- 假設我們要保留 Top 10% 的水準,我們就看這 16 條裡面的前 10% 分數是多少 (例如 0.8 分)。
- 這個 0.8 分 就變成了接下來所有路徑的生死門檻 (Threshold )。
Step 2: 線上處決 (The Kill Switch) —— 即時止損 接著開始大規模生成。在每一條路徑生成的過程中,系統會持續計算當前的 Group Confidence。
- 還記得 Group Confidence 是一個滑動視窗嗎?每生成一個字,我們都在算分數。
- 關鍵邏輯: 如果現在這一小段的分數已經低於門檻 (例如掉到 0.4 分),我們就可以斷定這條路徑最終的 Lowest Score 絕對不會高於 0.4。
- 行動: 既然這條路徑注定不及格,系統會立刻切斷生成 (Early Stop)。
- 效益: 這條路徑可能原本要寫 1000 個字,我們在第 200 字就殺掉它,直接省下了 800 個字的運算費!
Step 3: 自適應採樣 (Adaptive Sampling) —— 見好就收 我們還需要知道「什麼時候該停止生成新的路徑」。
- 每生成完一條有效路徑,我們就更新一次投票結果。
- 如果發現某個答案的得票率已經超過 95%(共識很高),代表大家意見一致,勝負已定。
- 這時,我們就停止整個任務,輸出答案。不需要為了湊滿 100 條而繼續浪費錢。
4 實驗結果: 數據會說話
DeepConf 的效果如何?論文在 AIME (數學競賽)、GPQA (研究生等級科學問答) 等高難度資料集上進行了測試,結果令人驚艷。
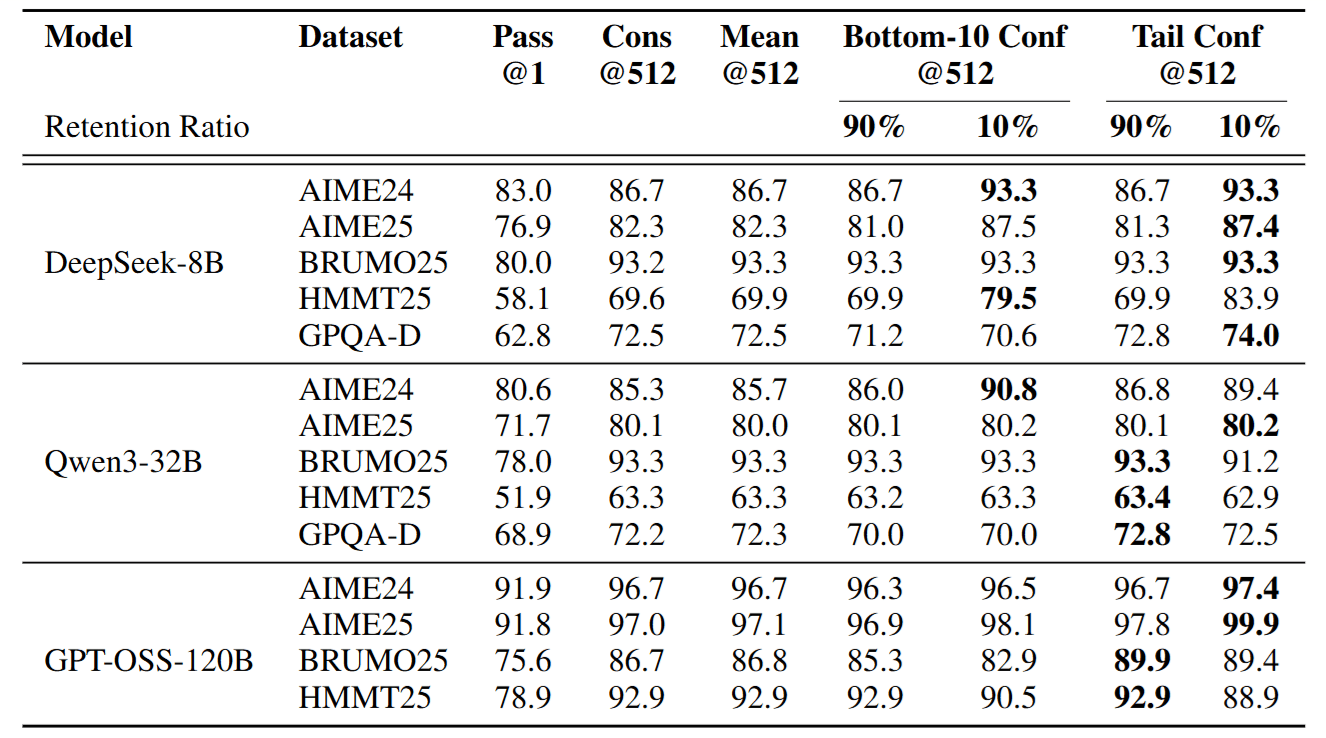
4.1 「少即是多」: 丟掉答案反而更準
在離線測試中,研究發現,如果我們丟掉 90% 的低信心路徑,只讓剩下 10% 的菁英進行投票,準確率往往比讓所有人投票還要高。
- 例如 DeepSeek-8B 在 AIME24 上,傳統投票準確率 86.7%,使用 DeepConf 篩選後提升至 93.3%。這證明了低信心的路徑大多是雜訊。
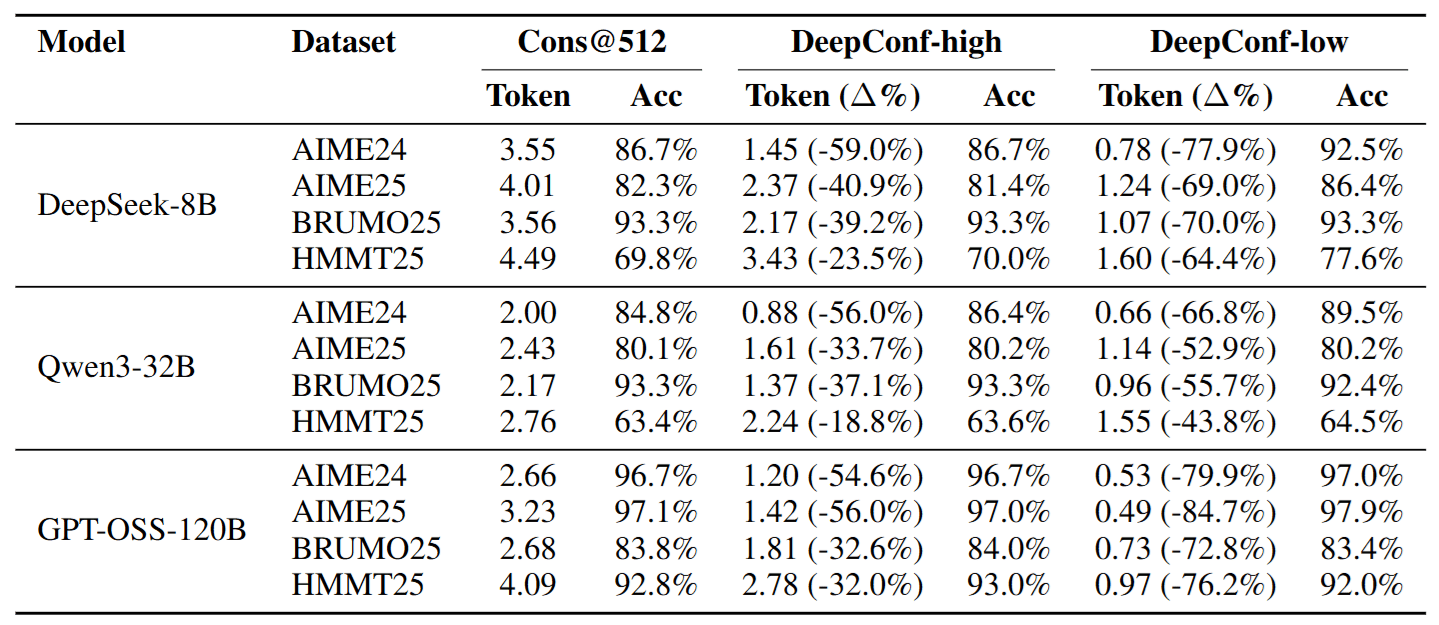
4.2 省錢奇蹟: 成本大降,效能不減
在線上測試中,DeepConf 展現了極致的效率。
- DeepConf-low (激進省錢版): 在某些任務上,能節省高達 84.7% 的 Token,同時準確率還能持平甚至提升!這意味著原本要跑 10 小時的任務,現在可能 2 小時就跑完了。
- DeepConf-high (保守穩健版): 在幾乎不犧牲任何準確率的情況下,穩定節省 20%~50% 的成本。
4.3 局部優於全局
實驗數據也證實,使用 Bottom-10% 或 Tail 這種關注「局部」和「短板」的指標,其分辨好壞的能力優於單純看整體的平均值。這驗證了「一條錯誤的推理往往源自於某個片段的崩潰」這一假設。
5 結論: 讓 AI 學會「適可而止」
Deep Think with Confidence (DeepConf) 並不是要訓練一個更強大的新模型,而是教導我們如何更聰明地使用現有的模型。
透過簡單的信心監控機制,DeepConf 成功解決了平行思維 (Parallel Thinking) 高昂成本的問題。它告訴我們:
- AI 是有「自知之明」的,它知道自己什麼時候在瞎掰。
- 與其讓 AI 盲目地生成大量文字,不如在它猶豫不決時即時喊卡。
- 這種「去蕪存菁」的過程,不僅省下了巨額的運算成本,往往還能讓最終的答案更加精準。
對於未來的 AI 應用開發者來說,這篇論文提供了一個極具價值的思路: 高品質的推理,不在於想得多,而在於想得「精」且「穩」。