你的 Base Model 其實比你想的更聰明！揭秘如何透過 MCMC 採樣讓模型超越 RL

2025-12-02 2026-07-20 約 10168 字預計閱讀 45 分鐘

深入解析《Reasoning with Sampling》論文，揭秘如何透過 MCMC 採樣與分佈銳化 (Distribution Sharpening)，讓 Base Model 不需強化學習 (RL) 也能展現驚人推理能力。探索 Inference-time Compute 如何以時間換取智能，解鎖模型隱藏潛力。

1 前言

本篇文章和大家分享 Reasoning with Sampling: Your Base Model is Smarter Than You Think 論文，該論文於 2025 年 10 月上傳至 arXiv，目前已經投稿到 ICLR 2026 會議，投稿結果尚未出爐! 但是從 Reviewer 給的分數來看，應該是篇很不錯的論文!

之所以想閱讀這篇論文的主要原因是－它挑戰了當前主流觀點 (Reinforcement Learning (RL) for Reasoning) 的論文，提出在 Inference 階段透過 Sampling 的方式，也可以讓 Base Model 達到甚至超越 RL Model 的 Reasoning 能力。

2 本篇論文想解決的問題

為了理解本篇論文想解決的問題，我們需要 (1) 理解 Distribution Sharpening 的概念以及 (2) 理解本篇論文對 RL 的假設。

2.1 什麼是 Distribution Sharpening

Distribution Sharpening 的中文稱為「分布銳化」是一種對機率分布的操作。

想像一下我們有一個 Base Model 在預測下一個 Token 或者生成一段完整的推理路徑時，它會有一個機率分布 $p(x)$ 。

有些回答的概率很高 (e.g. 合理的推理)
有些回答的概率很低 (e.g. 胡說八道)
還有很多回答介於中間

Sharpening (銳化) 就是通過數學運算，讓原本機率就高的地方變得更高，原本機率低的地方變得更低。

用數學公式來表示，如果我們有一個參數 $\alpha > 1$ ，Sharpening 後的機率 $p_{sharp}(x)$ 與原機率的關係是：

p_{sharp}(x) \propto p_{base}(x)^\alpha

以生活化的例子來看，這就像是用修圖軟體調整「對比度」:把灰色的地方變黑，亮灰的地方變白。在模型的世界裡，就是讓模型「更加相信」它原本就認為比較好的那些答案 (因為這些答案的機率變得更高)，同時極度壓抑那些它覺得不太好的答案 (因為這些答案的機率變得更低)。

2.2 本篇論文對 RL 的假設

這篇論文提到 Distribution Sharpening 是為了重新解釋 RL 在模型的推理能力中的影響。這是整篇論文的理論基礎!

目前像 OpenAI o1 或 DeepSeek-R1 這類強大的推理模型，都是通過 RL（e.g. PPO, GRPO）進行後訓練（Post-training）得到的。但學界有一個巨大的爭論：RL 到底有沒有讓模型學會「新」的推理能力？

觀點 A： RL 教會了模型以前不會的邏輯
觀點 B (本論文支持): RL 並沒有教會模型新東西，它只是把 Base Model 本身就隱含的、已經存在的正確推理路徑「挖掘」出來，並通過訓練把這些推理路徑的機率「銳化」(Sharpening) 了

因此，作者認為經過 RL 訓練的模型，其表現出來的行爲，其實就等同於一個 “Sharpened Base Model”。也就是說，Base Model 其實早就知道正確答案 (Smarter Than You Think)，只是這些正確的推理路徑被淹沒在大量平庸的推理路徑中，機率不夠突出。而透過 RL 訓練，等同於將 Base Model 進行 Sharpening，使得正確的推理路的機率變得更高，而錯誤的推理路徑的機率變得更低。

本篇論文的立場: Base Model 原本就知道答案

到目前為止，可以發現到本篇論文的立基點在於 Base Model 對於生成正確的推理路徑的機率比錯誤推理路徑來得更高。

因為在 Distribution Sharpening 的過程是具有單調性 (Monotonicity) 的，如果正確的推理路徑的機率真的低於錯誤的推理路徑，那麼單純的 Sharpening 也不會讓正確的推理路徑的機率大於錯誤的推理路徑。

我們已經知道： $p_{new}(x) \propto p_{old}(x)^\alpha$

如果對於兩個推理路徑，錯誤路徑 $x_{wrong}$ 和正確路徑 $x_{correct}$ ，在 Base Model 中滿足：

p(x_{wrong}) > p(x_{correct})

那麼，只要 $\alpha > 0$ ，銳化後依然會是：

p(x_{wrong})^\alpha > p(x_{correct})^\alpha

因此如果 Base Model 真的認為「錯誤推理路徑」的總機率 (Joint Probability) 比「正確推理路徑」高，那麼這篇論文的方法理論上無法讓模型穩定輸出正確答案。

這其實揭示了這種方法的邊界：它不能「無中生有」。如果 Base Model 對某個領域完全無知 (比如問一個文組模型怎麼解量子力學方程)，正確推理路徑的機率趨近於 0，那麼怎麼銳化都是 0。

為什麼論文敢聲稱 "Base Model is Smarter Than You Think"

理解本篇論文的立場 (Base Model 原本就知道答案 = Base Model is Smarter Than You Think) 後，你會不會覺得很奇怪，明明在我們的使用經驗中，Base Model 產生的輸出往往不如 SFT Model 或 RL Model 來得好，作者憑什麼相信 Base Model 這麼厲害?

這主要是因為 「Sampling的陷阱」!

很多時候，正確的推理路徑的機率 $p(x_{correct})$ 在全局 (Global) 上看，其實是比錯誤的推理路徑的機率 $p(x_{wrong})$ 高的，但是我們平常採樣不到。

為什麼？

Local Optima：
- 錯誤的推理路徑往往在開頭幾個 Token 機率很高 (像是模型很會講廢話)，使得一般的採樣方法 (e.g. Top-k, Nucleus Sampling) 走進去。一旦走進去，後面 Token 雖然機率掉下來了，但已經回不去了
- 正確路徑可能在開頭幾個 Token 機率普普 (由其是那些需要 “Pivot Token” 轉折的思考)，導致一般採樣選不到
Joint Likelihood：
- 這篇論文賭的是：雖然正確的推理路徑每一步不一定是最高的，但乘起來的總機率 (或者 Log-likelihood 的總和)，正確的推理路徑其實是最高的 (或者是局部最高峰之一)

總結來說，這篇論文敢聲稱 “Base Model is Smarter Than You Think” 是因為在 Base Model 中，經常正確的推理路徑的機率 $p(x_{correct})$ 其實是比錯誤的推理路徑的機率 $p(x_{wrong})$ 高的，只是整體機率或是以單一 Token 的角度來看都不夠突出，導致一般的採樣策略 (e.g. Top-k, Nucleus Sampling) 經常採樣不到這種正確的推理路徑。

回到本篇論文想解決的問題:

如果 RL 的本質僅僅是 Distribution Sharpening，那我們為什麼要花大錢去訓練? 我們能不能在推理階段（Inference Time）直接用算法模擬出這個銳化後的機率分布？

3 本篇論文提出的方法

一句話總結的話就是:

透過 Markov Chain Monte Carlo 方法從 Base Model 的 Sharpened Distribution 進行採樣

為了解決上述問題，本篇論文提出了 Distribution Sharpening 與 Inference-Time Sampling 方法。作者不想直接直接把 Base Model 訓練成 RL Model，而是將 Base Model 原本的機率分布 $p (x)$ 進行 Sharpening 後變成 $p (x)^\alpha$ 再對這個 Sharpened Distribution 進行 Sampling，來達到和 RL Model 一樣輸出表現。

注意，這裡的 $p (x)$ 指的是 Base Model 產生完整的推理路徑的機率 (也就是 Joint Probability)，而非產生單一 Token 的機率。這也就區隔了 “Sampling from a Sharpened Distribution” 和一般常見的 “Low-temperature Sampling” 的差異!

Sampling from a Sharpened Distribution vs Low-temperature Sampling

Sampling from a Sharpened Distribution (本論文提到的 $p^\alpha$ )： 是針對整個輸出序列（Output Sequence） 的機率 (也就是 Joint Probability) 做 Sharpening。從 $p^\alpha$ 採樣帶來的好處是，模型可能會在某一步選擇一個機率較低的 Token (e.g. Pivot Token)，因為這個 Token 雖然當下機率低，但它能開啟後面一連串高機率的正確的推理路徑
Low-temperature Sampling (我們平常用的 temperature < 1)： 是在每一步（per-token） 生成時做 Sharpening。它是貪婪的 (Greedy)，只看眼前這一步哪個 Token 機率高。這會導致模型陷入 Local Optima，選了眼前機率高但長遠來看是錯誤的推理路徑

如何計算 Joint Probability?

以數學的角度上來看，就是把模型對於完整推理路徑中的每一個 Token 的輸出機率相乘在一起，但在電腦裡為了避免數值太小溢位，我們會取 Log 變成相加。

機率定義： $P(\text{Trace}) = P(token_1) \times P(token_2 | token_1) \times P(token_3 | token_{1,2}) \dots$
論文的 Joint Probability $p(x)^\alpha$ ： 就是把上面那一長串乘積，再取 $\alpha$ 次方。
實作層面（Log-Likelihood）： 我們會看模型的 Logits 或 Log-Probs。 $\log P(\text{Trace}) = \sum \log P(token_i | \text{previous})$

3.1 為什麼要用 Markov Chain Monte Carlo

到目前為止，我們理解了作者的目標是從 Sharpening 後的機率分布 $p(x)^\alpha$ 中採樣，且這個 $p(x)^\alpha$ 指的是整條推理路徑 的機率而非單一 Token 的機率。

那麼問題就來了，假設詞彙表大小是 $V$ ，生成的完整推理路徑的長度是 $T$ ，那可能的推理路徑總數就會是 $V^T$ 。這是一個天文數字。

要直接從一個機率分布採樣，通常我們會需要知道每個可能的推理路徑的 Normalized Probability：

P_{target}(x) = \frac{p(x)^\alpha}{Z}

這裡的 $Z$ (Normalization Constant) 是所有可能推理路徑的機率總和:

Z = \sum_{all \ possible \ traces} p(x)^\alpha

問題來了我們根本算不出 $Z$ ，因為有 $V^T$ 種可能的推理路徑。但是我們可以很容易地算出分子 $p(x)^\alpha$ 。因為 $p(x)$ 就是 Base Model 對這個推理路徑的 Likelihood，這是模型 Forward Pass 一次就能計算出來的 Joint Probability。

這裡正是為什麼需要使用 Markov Chain Monte Carlo 的關鍵，Markov Chain Monte Carlo 這類算法最強大的地方在於：**它不需要知道 $Z$ ，只需要知道「兩個樣本之間的相對強弱」，就能從目標機率分布中採樣。**換句話說，透過 Markov Chain Monte Carlo，我們不需要真的計算所有可能推理路徑的機率再進行 Sharpening 然後再採樣；我們只要可以計算出任意兩個推理路徑的 $\frac{p(x_{new})^\alpha}{p(x_{old})^\alpha}$ ，Markov Chain Monte Carlo 就能運作。

3.2 什麼是 Markov Chain Monte Carlo

Markov Chain Monte Carlo 從字面上來看可以拆解為兩個部分:

Monte Carlo: 指的是通過「隨機抽樣」來解決問題的方法
Markov Chain: 我們設計一個狀態機，讓它在不同的狀態（這裡是不同的推理路徑）之間跳來跳去

核心思想： 我們不想要憑空生成一個完美的推理路徑 (太難了)，我們想要構建一個 Markov Chain，使得當這個 Chain 運行足夠久之後，它停留在某個狀態 (推理路徑) 的頻率，剛好等於我們想要的目標機率 $p(x)^\alpha$ 。

這就像是設計一個機器人，讓它在一個充滿著推理路徑的空間裡隨機漫步。我們給它設下規則：

如果走到「好的推理路徑 (高機率)」的地方，就多逗留一會兒
如果走到「爛的推理路徑 (低機率)」的地方，就快點離開，或者乾脆別過去

最終，我們記錄下這個機器人走過的所有狀態，這些狀態就是符合從 $p(x)^\alpha$ 這個機率分布所採樣出來的樣本。

3.3 Markov Chain Monte Carlo 經典演算法－ Metropolis-Hastings

這篇論文具體使用的是 Markov Chain Monte Carlo 家族中最經典的 Metropolis-Hastings 演算法。

它的運作流程非常直觀，分為三步：

Step 1: Current State

假設我們手上已經有一個生成的推理路徑，我們叫它 $x$ (e.g. 一個普通的解題過程)。

Step 2: Proposal

我們需要一個機制來「隨機修改」這個推理路徑，產生一個候選的新句子 $x'$ 。因此，我們會隨機選一個位置 $t$ ，把 $t$ 後面的字全部砍掉，讓 Base Model 重新生成 (Resample) 後半段。這個「重新生成」的過程，我們稱為 Proposal Distribution $q(x'|x)$ 。

Step 3: Accept or Reject

這是最關鍵的一步！我們要決定: 是跳到新句子 $x'$ ，還是留在舊句子 $x$ ? 因此，我們會計算一個 Acceptance Ratio $A$ :

A(x', x) = \min \left( 1, \frac{p(x')^\alpha}{p(x)^\alpha} \times \frac{q(x|x')}{q(x'|x)} \right)

我們看它的物理意義：

Likelihood Ratio ( $\frac{p(x')^\alpha}{p(x)^\alpha}$ ):
- 如果新的推理路徑 $x'$ 的分數比舊句子 $x$ 高，這個值就大於 1
Proposal Correction ( $\frac{q(x|x')}{q(x'|x)}$ ):
- 這是為了修正 Proposal 這個動作本身的偏差 (如果是對稱的，這項通常為 1)

規則：

計算出 $A$ 之後，我們生成一個 0 到 1 的隨機數 $u$
如果 $u < A$ ，我們就接受 (Accept) 新句子，狀態變成 $x'$
否則，我們就拒絕 (Reject)，狀態保持在 $x$ (也就是再來一次)

3.3.1 砍掉幾個 Token? $t$ 該怎麼設定?

理論上，我們可以直接砍掉最後的 $t$ 個 Token。但在論文中提出的演算法 (Algorithm 1) 中，策略稍微精細一點，它是分塊 (Block) 進行的。

分塊生成 (Sequential Block)：
作者並不是一次生成幾百個 Token 的完整 Trace 然後才開始 Markov Chain Monte Carlo。它是把長度 $T$ 切成很多小塊 (Block)，每塊長度為 $B$ （例如 $B=192$ token）。
1. 先生成第一個 Block
2. 對這「第一個 Block」進行 Markov Chain Monte Carlo 優化 (重複砍掉重練)
3. 滿意了 (或次數到了)，把這個 Block 固定 (Fix) 下來
4. 接著生成第二個 Block……以此類推
在這個 Block 內怎麼砍?
在針對當前 Block 進行 Markov Chain Monte Carlo 時，它是隨機選擇一個切點 $m$ 。
- 比如當前 Block 有 192 個 Token
- 這一次迭代 (Iteration) 可能隨機選中第 50 個 Token，把 50 之後的全部砍掉重算
- 下一次迭代可能選中第 180 個 token，只重算最後一點點
因此 $t$ 不是固定的，是在當前處理的 Block 範圍內隨機選取切點，然後重算該點之後的所有內容。

3.3.2 整個過程重複幾次? 什麼時候停止?

理論上的 Markov Chain Monte Carlo 是要跑無限次才會完美收斂，但在工程上我們有計算預算(Compute Budget)。

參數設定： 論文中有一個參數叫做 $N_{MCMC}$
流程： 對於每一個 Block (e.g. 192 個 Token)，我們強制跑 $N_{MCMC}$ 次的「重算 -> 比較」循環
停止條件： 跑完 $N_{MCMC}$ $N_{MCMC}$ 次 (e.g. 10 次或 20 次)，我們就假設現在手上的這個 Trace 已經夠好了，就把它固定下來，往下一個 Block 前進
- 並不是「達到某個機率」才停 (因為我們不知道最高機率是多少)，而是「時間到了」就停

3.3.3 憑什麼保證 Markov Chain Monte Carlo 能找到正確的 Trace? 如果 Propose 的更爛怎麼辦?

Markov Chain Monte Carlo 的保證來自於 「接受/拒絕 (Accept/Reject)」機制 和 「隨機性」 的博弈。

情況 A: Propose 的新 Trace 機率比原本的高 (代表得到品質更好的推理路徑)
- 根據公式，接受率 $A > 1$
- 我們 100% 接受 這個新的。這就像爬山，看到高處一定往上爬
- 結果： 我們手上的 Trace 變強了
情況 B：Propose 的新 Trace 機率比原本的低(代表得到品質更差的推理路徑)
- 這是常態，因為亂改通常會改壞
- 根據公式，接受率 $A < 1$ (例如 $A=0.1$ )
- 我們有 $10\%$ 的機率接受它，有 $90\%$ 的機率 拒絕它 (Reject)
- 關鍵點： 如果拒絕了，我們是退回到原本那個比較好的狀態，而不是停在爛的狀態。所以我們手上的 Trace 最差也就是保持原樣
為什麼會收斂？ 雖然 Proposal 經常給出爛的，但只要 Base Model 有非零的機率生成出那個「好的 Trace」，在嘗試足夠多次後，總有一次會「矇對」一個更好的片段。一旦矇對了 (情況 A)，我們就會接受並鎖定它，把它當作新的基準 (Baseline)。下一次就要找出比這個更好的才能更新。這就像是一個帶有保險機制的隨機嘗試：改好了就留著，改壞了就復原 (大機率)。

3.3.4 計算 Acceptance Ratio $A$ 中的 Likelihood Ratio 為什麼需要使用 Sharpening 參數 $\alpha$ ?

在計算 Acceptance Ratio $A$ 中：

A(x_{new}, x_{old}) = \min \left( 1, \frac{p(x_{new})^\alpha}{p(x_{old})^\alpha} \right) = \min \left( 1, \left( \frac{p(x_{new})}{p(x_{old})} \right)^\alpha \right)

如果 $\alpha = 1$ (沒 Sharpening)：
如果新句子機率是舊句子的 2 倍，接受率是 2 (必接受)。如果新句子機率是舊句子的 0.5 倍，接受率是 0.5。
如果 $\alpha = 4$ (高 Sharpening，論文常用值)：
如果新句子機率是舊句子的 2 倍，接受率變成 $2^4 = 16$ (超級必接受)。如果新句子機率是舊句子的 0.5 倍，接受率變成 $0.5^4 = 0.0625$ 。

結論： $\alpha$ 決定了我們對「好壞」的敏感度。 $\alpha$ 越大，演算法就越「勢利眼」：極度渴求高分句子，極度排斥低分句子。這正是強迫模型往高機率區域（正確推理）收斂的推動力。

3.3.5 為什麼在 (Step 3) Accept or Reject 的過程不直接 “總是” 選擇機率大的推理路徑? 還需要計算接受率?

這是 優化 (Optimization) 與 採樣 (Sampling) 之間最本質的區別，如果我們的目標純粹是只選機率大的，這叫做 Hill Climbing / 爬山演算法，那在這個情況我們甚至不需要 $\alpha$ ，也不需要接受率的計算，只要寫 if new > old then accept 就好了。

但這篇論文之所以要用 Markov Chain Monte Carlo 且必須加上 $\alpha$ ，有兩個無法被「只選大的」取代的理由：

為了跳出 Local Optima
如果你採取「只選機率大的 (Deterministic)」策略:
- 情境： 你現在在一個小山丘的頂端 (Reasoning Trace 尚可，但不是最佳)
- 問題： 任何的修改 (Proposal) 都會導致機率暫時下降 (往山下走一步)
- 結果： 因為你的規則是「只選大的」，你會永遠拒絕這些修改。你會被困死在這個小山丘上，永遠到不了旁邊那座更高的聖母峰 (正確答案)
Markov Chain Monte Carlo 的智慧:
它允許你偶爾接受比較差的結果 (機率性接受)。
- 這就像爬山時，允許你先「下坡」一段路，這樣你才有機會跨過山谷，去爬對面那座更高的山。
$\alpha$ 在這裡的角色： 如果不加 $\alpha$ (e.g. $\alpha=1$ )，Markov Chain Monte Carlo 太容易接受差的結果了 (太容易下坡)，導致在錯誤的路徑上浪費太多時間。加上 $\alpha$ (e.g. $\alpha=4$ )，我們把機率差距拉大。
- 對於「稍微差一點點」的路徑: 接受率只是稍微降低，還有機會跳過去。
- 對於「差很多」的路徑：接受率會指數級暴跌，幾乎不可能接受。
所以， $\alpha$ 是用來控制 我們願意冒多大風險去探索 (Explore) 的參數。
數學上的必要性
這點回到論文標題：Distribution Sharpening。我們要模擬的目標分佈不是 Base Model 原本的 $p(x)$ ，而是銳化後的 $p(x)^\alpha$ 。
根據 Metropolis-Hastings 的數學推導，Acceptance Ratio $A$ 必須等於 「目標機率的比值」。
$A = \frac{\text{Target}(x_{new})}{\text{Target}(x_{old})}$
- 如果我們的目標是 $p(x)$ ，那比值就是 $\frac{p(x_{new})}{p(x_{old})}$
- 但我們的目標是 $p(x)^\alpha$ ，所以比值必須是： $\frac{p(x_{new})^\alpha}{p(x_{old})^\alpha} = \left( \frac{p(x_{new})}{p(x_{old})} \right)^\alpha$
這個數學動作帶來的物理意義：
$\alpha$ 就像一個「放大鏡」或「對比度旋鈕」。
假設 $x_{new}$ 比 $x_{old}$ 好一點點，機率是原本的 $1.2$ 倍
- 沒有 $\alpha$ ： 接受率 $1.2$ 。優勢只有 20%
- 有 $\alpha=4$ ： 接受率 $1.2^4 \approx 2.07$ 。優勢變成了 107%
假設 $x_{new}$ 比 $x_{old}$ 差一點點，機率是原本的 $0.8$ 倍。
- 沒有 $\alpha$ ： 接受率 $0.8$ 。你有 80% 的機率會接受這個變差的結果 (太容易動搖了)
- 有 $\alpha=4$ ： 接受率 $0.8^4 \approx 0.41$ 。你只剩下 41% 的機率接受它

總結：

你需要 $\alpha$ 參數，是因為：

演算法行為： $\alpha$ 讓演算法對「好壞」更敏感。它強迫模型「更貪婪一點，但又不完全死板」
數學定義： 你的目標就是 Sharp Distribution，公式規定比值要帶次方

3.3.6 Metropolis-Hastings 中的 Proposal Correction 是什麼?

簡單來說，這個項是為了「公平性（Fairness）」而存在的。

我們看公式中的這部分：

\frac{q(x_{old} | x_{new})}{q(x_{new} | x_{old})}

分母 (Forward): 從舊的路徑 $x_{old}$ 跳到新的路徑 $x_{new}$ 有多容易?
分子 (Backward): 如果我們已經在新的路徑 $x_{new}$ ，想跳回舊的 $x_{old}$ 有多容易?

為什麼需要這個修正? (直覺解釋)
想像我們在玩一個遊戲，要隨機參觀不同的房間 (推理路徑)。我們的目標是去參觀那些「漂亮的房間」(機率高的推理路徑)。
但是，我們的移動方式 (Proposal) 有偏差：
- 有些房間有 10 個入口，很容易不小心走進去
- 有些房間只有 1 個入口，很難發現它
如果我們不修正這個偏差，我們就會誤以為那些「入口多」的房間比較漂亮，導致我們在那裡待太久。
Proposal Correction 就是在消除這種「入口數量」造成的偏差。
- 如果一個新路徑 $x_{new}$ 是很容易被生成出來的 (分母很大)，這代表這個 Proposal 本身就偏心它。為了公平，我們要在公式裡扣分 (除以一個大數)
- 反之，如果一個新路徑是很難得才生成出來的，我們就要加分
這樣一來，我們最終是否留在這個房間，就只取決於房間漂不漂亮 ( $p^\alpha$ )，而不是取決於門好不好進。
在這篇論文中，這代表什麼? (數學推導)
在這篇論文的算法裡，這一項有非常特殊的數學效果。
- Proposal ( $q$ ): 作者直接用 Base Model 來生成新片段。所以生成某個新後綴 (suffix) 的機率，其實就是 Base Model 原本的機率 $p(suffix)$ 。
讓我們把這個代入公式看看 (為了簡化，假設 Prefix 固定):
1. 目標比率 (Target Ratio): 我們想要的比值。
  $\frac{p(x_{new})^\alpha}{p(x_{old})^\alpha}$
2. 修正項 (Correction Term):
  - 從 Old 跳到 New 的機率 $\propto p(x_{new})$ (因為是 Base Model 生成的)
  - 從 New 跳回 Old 的機率 $\propto p(x_{old})$
  - 所以修正項是： $\frac{p(x_{old})}{p(x_{new})}$
3. 最終的接受率 (Acceptance Ratio):
  $A = \underbrace{\left( \frac{p(x_{new})}{p(x_{old})} \right)^\alpha}_{\text{我們想要的}} \times \underbrace{\left( \frac{p(x_{old})}{p(x_{new})} \right)}_{\text{修正項}}$
  利用指數律合併一下：
  $A = \left( \frac{p(x_{new})}{p(x_{old})} \right)^{\alpha - 1}$
從這個結果我們可以發現，如果不加修正項，我們傾向於接受那些 Base Model 覺得機率高的句子 (因為 Proposal 會一直推銷這些句子)。加了修正項之後，我們把 Base Model 原本的偏好 (Bias) 抵消掉了一次 (減 1)。

4 本篇論文的實驗結果

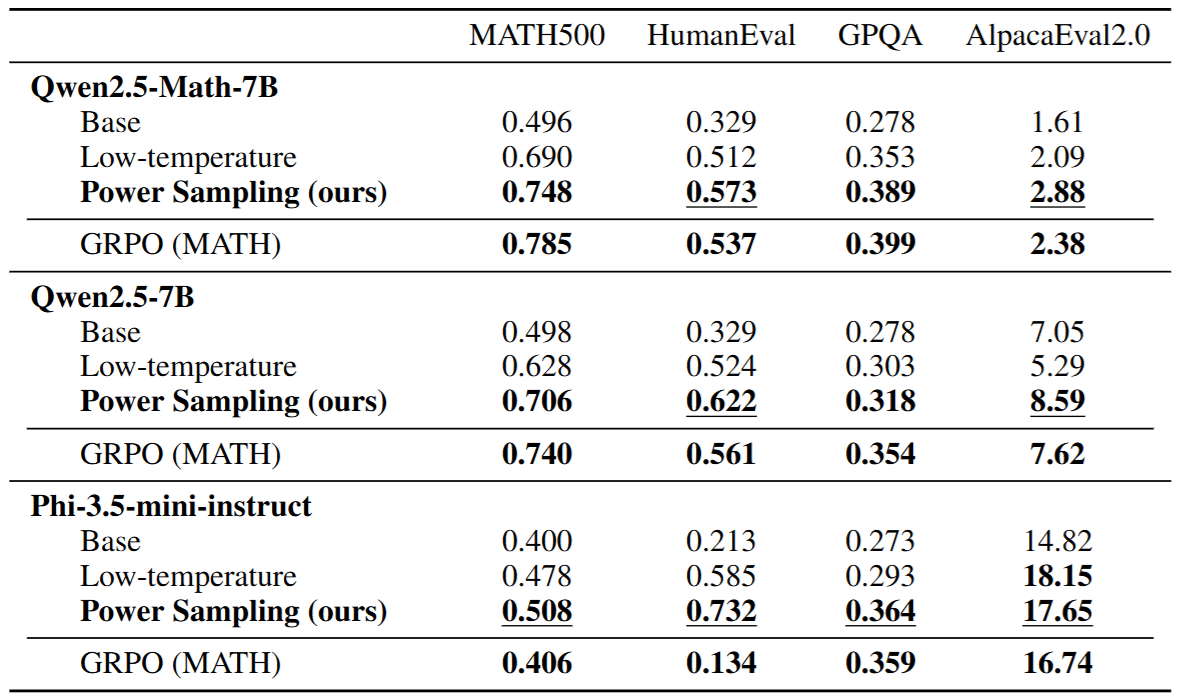
在 MATH500、HumanEval、GPQA 與 AlpacaEval2.0 上針對 Qwen2.5-Math-7B、Qwen2.5-7B 與 Phi-3.5-mini-instruct 的結果表格，比較 base、低溫度、Power Sampling 與 GRPO，Power Sampling 在不需訓練的情況下接近甚至有時超越 GRPO — 本篇論文提出的 Power Sampling 方法與 GRPO 在多個 Benchmark 上的比較

最後則是附上本篇論文的主要實驗結果，可以發現單純針對 Base Model 進行 Sampling 的作法確實在許多 Benchmark 上達到甚至超越 RL (e.g. GRPO) Model 的表現。

5 結語

本篇文章和大家分享 Reasoning with Sampling: Your Base Model is Smarter Than You Think 論文，不管是在閱讀還是撰寫本篇文章時，都覺得滿滿的收穫！

我覺得最有趣的方，不僅僅是它提出了一套基於 Markov Chain Monte Carlo 的採樣算法，而是它在哲學層面上對當前 AI 發展路徑提出了一個反思：我們是否低估了 Base Model 的潛力，而過度神話了 RL 的作用?

回顧整篇文章，我們可以歸納出三個值得深思的觀點：

5.1 推理的本質：是「學習」還是「搜尋」？

過去我們傾向認為，模型需要透過 RL (e.g. PPO, GRPO) 才能「學會」邏輯推理。但本篇論文透過 Distribution Sharpening 的視角告訴我們，或許推理能力的本質更像是一種從雜訊中提取訊號的過程。

Base Model 就像是一個讀過萬卷書但缺乏自信的學生，正確答案其實就在他的腦海裡 (Latent Space)，只是被淹沒在大量平庸的回答中。我們不需要透過 RL 重新教他知識，只需要給他一點時間、一點引導 (Sharpening & Sampling)，讓他有機會去反覆推敲，正確的推理路徑自然會浮現。這正是標題 “Your Base Model is Smarter Than You Think” 的真諦。

5.2 Inference-time Compute 的崛起 (System 2 Thinking)

這篇論文的方法其實是 Inference-time Compute (推理時計算) 趨勢的完美體現。

System 1 (快思考)： Base Model 的直接輸出，依靠直覺，速度快但容易出錯
System 2 (慢思考)： 本文提出的 MCMC Sampling，依靠反覆推敲、回溯與修正，速度慢但邏輯嚴密

雖然 Markov Chain Monte Carlo 需要花費比平常更多的 Inference 時間與算力 (因為要不斷 Propose 和 Reject)，但這也意味著我們可以透過**「用時間換取智能」(Trading Time for Intelligence)**。在不需要重新訓練龐大模型的情況下，僅僅透過改變採樣策略就能解鎖強大的推理能力，這對於資源有限的研究者或企業來說，無疑是一條極具吸引力的道路。

5.3 未來的展望：RL 與 Sampling 的共舞

當然，這並不代表 RL 將被淘汰 (怎麼可能 XD)。作者也提到，如果 Base Model 對某個領域完全一無所知 (機率為 0)，那麼再強的 Sharpening 也無濟於事。

說不定未來的趨勢可能會走向一種混合模式: 利用 RL 進行輕量級的對齊，確保 Base Model 的機率分布大方向正確；然後在 Inference 階段，針對高難度的推理問題，動態地引入像本篇論文提出的 Markov Chain Monte Carlo 策略來進行深度搜索。

這種單一鏈的 MCMC 做法也值得和 DeepConf 對照 — DeepConf 把 Inference-Time 的運算預算花在不同的地方：同時生成大量平行的推理路徑，再透過 Token 層級的信心分數提早砍掉表現不佳的路徑，而不是反覆優化單一路徑。

總而言之，是一有趣且很棒的論文，希望本篇文章對你也有帶來幫助!

目錄

目錄

你的 Base Model 其實比你想的更聰明！揭秘如何透過 MCMC 採樣讓模型超越 RL

1 前言