不微調、不靠 GPT-4！微軟 rStar 如何透過 MCTS 讓 LLaMA2-7B 數學能力暴增 5 倍？ (ICLR 2025)

1 前言

本篇文章要和大家分享的是 Microsoft Research Asia 與 Harvard University 合作的精彩論文: Mutual Reasoning Makes Smaller LLM Stronger Problem-Solvers (rStar)。這篇論文於 2024 年 8 月發表，並已成功收錄為 ICLR 2025 Poster！

在 LLM 的發展歷程中，我們常認為要提升小參數模型 (SLMs，e.g. LLaMA2-7B) 的推理能力，必須依賴強大模型 (如 GPT-4) 的數據蒸餾來進行微調 (SFT)。但這篇論文提出了一個顛覆性的觀點: 小模型其實已經具備足夠的潛力，只是缺乏正確的「思考引導」與「自我驗證」機制。

作者提出了一種名為 rStar 的架構，結合了 MCTS (蒙地卡羅樹搜索) 與獨特的 Mutual Reasoning 機制。令人驚豔的是，在完全不需要微調、也不依賴 GPT-4 的情況下，僅透過推論階段的算法增強，就能讓 LLaMA2-7B 在 GSM8K 數學數據集上的準確率從 12.51% 暴增至 63.91%，甚至讓 Mistral-7B 超越了許多經過專門微調的模型。

接下來，我們將深入剖析 rStar 是如何透過模仿人類的思維動作 (Action Space) 以及像同學般的互相檢查 (Discriminator)，解鎖小模型的深層推理能力。

2 rStar 想解決的問題

以大方向來說:

如何讓小模型 (SLMs) 在不依賴更強大模型 (如 GPT-4) 蒸餾數據的情況下，顯著提升自身的推理能力。

我們可以將 rStar 想解決的問題歸納為以下三個層次:

2.1 宏觀挑戰: 小模型的推理能力瓶頸與對「老師」的依賴

• 現狀: 小參數語言模型 (SLMs，例如 Mistral-7B, LLaMA2-7B) 在複雜推理任務 (如 GSM8K 數學題) 上的表現遠不如大模型。即使使用了 Chain-of-Thought (CoT)，準確率依然有限 (例如 Mistral-7B 只有 36.5%) 。
• 問題: 目前提升 SLM 推理能力的主流方法是 Fine-tuning (微調)，但這通常需要依賴「更強大的模型」 (如 GPT-4) 來生成高質量的合成數據或進行知識蒸餾。
• 目標: 論文希望打破這種依賴，實現 “Reasoning improvements without a superior teacher LLM”，即讓模型在 推理階段 (Inference-time) 通過自我博弈 (Self-play) 來提升能力，而不需要額外的訓練或外部監督。

2.2 技術挑戰 I: 生成階段的「無效探索」 (Ineffective Exploration)

當模型嘗試自我改進 (例如使用 RAP 等方法進行樹搜索) 時，面臨以下困難:

• 搜索空間陷阱: SLM 的能力有限，如果只是簡單地讓它「生成下一步」，它往往會在低質量的推理空間中打轉。論文中提到，即便讓 LLaMA2-7B 用 RAP 方法探索 32 輪，只有 24% 的軌跡是正確的。
• 動作空間 (Action Space) 單一: 傳統的 MCTS (蒙地卡羅樹搜索) 應用在 LLM 上時，動作通常很單一 (例如「提出下一個子問題」) 。這限制了模型模擬人類多樣化推理思維的能力 (如拆解問題、重新表述問題、一步推理 vs 多步推理等) 。

2.3 技術挑戰 II: 驗證階段的「盲目自信」 (Unreliable Verification)

即便模型生成了多條推理路徑，如何從中選出正確的那一條也是個大問題:

• 自我驗證的困難: 研究表明，SLM 很難準確評估自己生成的答案是否正確 (Self-verification is hard)。模型往往無法區分高質量和低質量的推理步驟。
• 多數決的局限: 傳統的 Self-Consistency (SC) 依賴「多數決 (Majority Voting) 」，這假設模型大部分時候是對的。但在難題上，SLM 可能大部分生成的答案都是錯的，導致多數決失效。
• 獎勵模型的成本: 如果要訓練一個專門的 Reward Model (RM)，又回到了需要標註數據或外部監督的問題，且容易 Overfitting (過擬合) 特定任務。

總結來說:

這篇論文要解決的核心痛點是:

小模型在「生成」時想不到好思路，在「檢查」時又分不清對錯。

rStar 試圖通過改進 MCTS 的動作空間 (讓生成更像人) 以及引入「互助推理」(Mutual Reasoning，讓另一個同級模型來驗證) 來解決這兩個問題。

3 rStar 所提出的方法

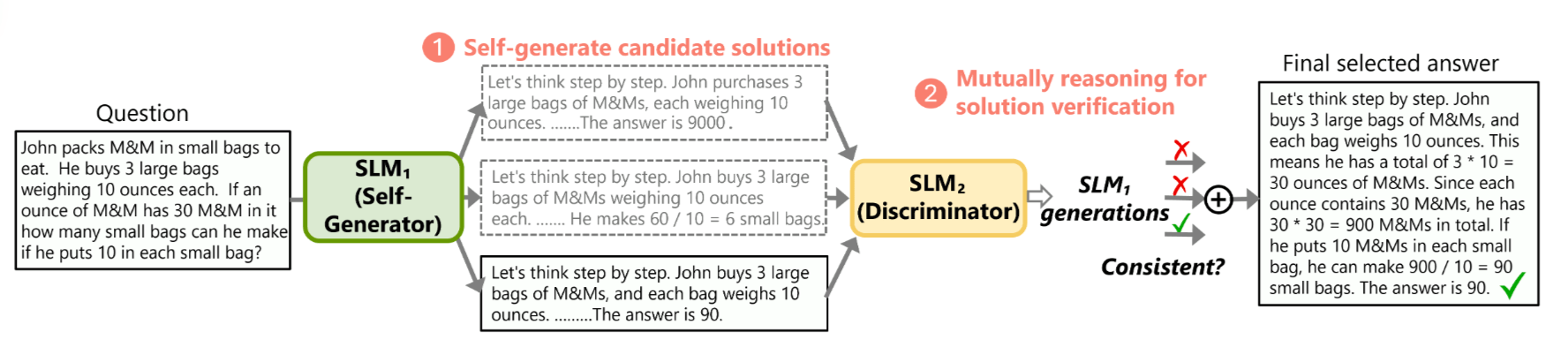
這篇論文提出的 rStar 方法可以用這句話來總結:

rStar 就像是讓小模型「分飾兩角」，一個角色 (稱之為 Generator) 利用模仿人類的多樣化思考策略 (如拆解問題、換句話說) 來生成解題路徑，另一個角色 (稱之為 Discriminator) 則像同學一樣通過「填空測試」來檢查這些路徑是否合理，兩者通過互相驗證 (Self-play) 在不重新訓練的情況下大幅提升推理準確率。

理解 MCTS (蒙地卡羅樹搜索) 是讀懂這篇論文技術細節的關鍵。rStar 的核心骨架就是建立在 MCTS 之上的。因此，我們會先從 MCTS 的基本概念談起，再接著說明 rStar 如何針對 MCTS 的每個階段設計方法。

3.1 MCTS 的基本概念 (四個階段)

MCTS 是一種啟發式 (Heuristic) 的搜索算法，最早在圍棋 (Go) 等博弈遊戲中大放異彩 (比如 AlphaGo)。它的核心思想是:

因為可能的路徑太多了，我不可能全部算完，所以我透過「隨機模擬」來統計勝率，把計算資源集中在「最有希望」的路徑上。

在 rStar 這篇論文中，MCTS 被用來幫助 Generator 生成推理步驟。一棵樹的根節點 (Root) 是問題，節點 (Node) 是中間的推理步驟，邊 (Edge) 是採取了某種動作 (Action) 。

MCTS 的一次迭代 (Iteration) 包含以下四個標準階段:

1. 選擇 (Selection):

   • 做什麼: 從根節點出發，沿著樹往下走，直到走到一個「還沒完全展開」的節點 (Leaf node)。
   • 怎麼選: 這一步不是隨機的，而是根據一個公式 (通常是 UCT, Upper Confidence Bound for Trees)。這個公式在平衡兩件事:
     • Exploitation: 走那條目前看起來分數最高、勝率最大的路。
     • Exploration: 走那條很少被走過的路，因為那邊可能藏著更好的答案。
   • 意義: 確保我們既關注當前最好的解，又不放棄探索未知的可能性。

2. 擴展 (Expansion):

   • 做什麼: 當「選擇」走到一個葉節點後，如果這個節點還能繼續往下推導，我們就創建一個或多個新的子節點 (Child Node)。
   • 意義: 在 rStar 中，這代表模型根據當前的推理狀態，採取了一個新的推理動作 (比如拆解問題、生成下一步)，長出了新的推理步驟。

3. 模擬 (Simulation / Rollout):

   • 做什麼: 從剛剛擴展出的新節點開始，快速地往後走到底，直到遊戲結束或生成完整答案。這通常使用比較簡單或隨機的策略 (Default Policy) 。
   • 意義: 這就像是「試跑」。因為只生成了一半的推理步驟不知道對錯，我們乾脆讓模型快速把剩餘步驟寫完，看看最後能不能得出一個合理的答案。

4. 反向傳播 (Backpropagation):

   • 做什麼: 根據「模擬」的結果 (比如最終答案是否通過了某種檢查，或者得到的 Reward 分數) ，將這個分數一路回傳給路徑上經過的所有父節點。
   • 意義: 更新這條路徑上所有節點的統計數據 (訪問次數 $N$ 和 價值 $Q$) 。如果這次模擬成功了，這條路徑上的節點分數就會變高，下次「選擇」階段就更容易被選中。

3.2 rStar 中的 “Selection” 流程

rStar 並沒有特別針對 Selection 做特別的設計，主要遵循原來的 MCTS 作法:

1. 從根節點出發: 從題目 (Root) 開始。
2. 面對分岔路: 假設當前節點已經擴展過 (Expanded)，有生成好幾個候選的 Child Node ($s_1, s_2, s_3...$)。
3. 打分數: 對每一個候選的 Child Node 計算 UCT 分數。
4. 挑選: 選擇 UCT 分數最高的那個 Child Node，移動過去。
5. 重複: 在新的 Node 繼續重複步驟 2-4，直到遇到一個「葉節點」(Leaf Node)，也就是一個還沒有生成過後續步驟的節點。

一旦到達葉節點，Selection 階段結束，接下來就會進入 Expansion (擴展) 階段。

3.2.1 UCT (Upper Confidence Bounds for Trees)

在 Selection 階段中，UCT (Upper Confidence Bounds for Trees) 分數該怎麼計算? 我們直接來看論文第 3.2 節 (Solution Generation with MCTS Rollout) 中的公式:

這個公式決定了 MCTS 在 Selection (選擇) 階段，面對多個可能的下一步 (Child Node) 時，該挑哪一個往下走。它由兩部分組成: 利用 (Exploitation) 和 探索 (Exploration)。

3.2.1.1 第一項: 利用 (Exploitation) —— 挑選「績優股」

• 含義: 這是節點 $s$ 的平均勝率 (平均獎勵)。

• $Q(s, a)$: 該節點累積的總分。

  Q(s, a) 的意義

  所以 $Q(s, a)$ 的準確含義是:

  「這個特定的推理步驟 $s$ (它是通過動作 $a$ 生成的) 所累積的總獎勵值。」

  • 場景模擬: 假設你現在在「第 1 步」，你正在考慮要不要選「第 2 步 (方案A)」。
  • 這裡的 $s$ 就是「第 2 步 (方案A)」。
  • $a$ 就是產生方案 A 的那個動作 (例如「提出一個子問題」)。
  • $Q(s, a)$ 就是歷史上我們經過這個節點 $s$ 後，最終判定它對解題有幫助的總得分。

• $N(s, a)$: 該節點被訪問過的次數。

• 直觀理解: 如果這個推理步驟我們之前走過 10 次，其中 9 次都導向了正確答案，那它的平均分數就會很高。這一項鼓勵模型去走那些過去經驗證明是好路的方向。

3.2.1.2 第二項: 探索 (Exploration) —— 給「潛力股」機會

• 含義: 這是給少走的路加分 (探索紅利)。
• $N_{parent}(s)$: 父節點 (當前所在的節點) 被訪問的總次數。
• $N(s, a)$: 子節點 $s$ (我們正在評估的候選人)被訪問的次數。
• 數學機制:
  • 分母是 $N(s, a)$: 如果這個節點 $s$ 我們已經走過很多次了，分母變大，這一項的值就會變小 (探索紅利降低)。
  • 分子是 $\ln N_{parent}(s)$: 隨著我們經過父節點的次數越來越多，如果某個子節點 $s$ 的訪問次數 $N(s, a)$ 一直沒增加(還是 0 或很小)，這個數值就會變得很大。
• $c$ (Constant): 這是一個超參數 (常數)，用來調節探索的權重。$c$ 越大，模型越喜歡嘗試新鮮的路徑。
• 直觀理解: 這一項在說: 「嘿！雖然旁邊那條路 (節點 $s$) 目前的平均分可能不是最高，或者是 0，但那是因為我們還沒怎麼走過它！給它一點機會試試看嘛！」

3.3 rStar 中的 “Expansion” 流程

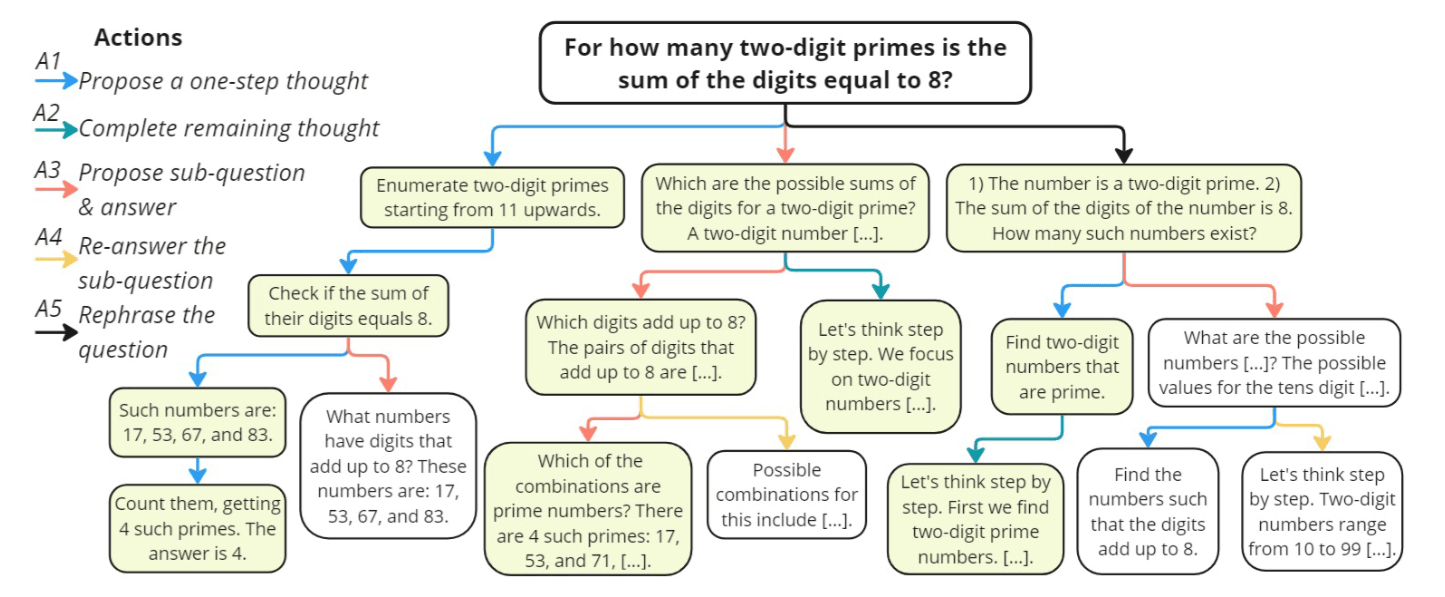
這正是這篇論文最精彩的創新點之一！傳統的 MCTS 往往只會用一種方式來「擴展」(比如: 永遠只問「下一步是什麼？」) ，但 rStar 觀察到人類在解難題時，思維方式是非常靈活多變的。

在 Expansion (擴展) 階段，當 MCTS 走到一個葉節點 (目前的推理狀態) 時，它會從 5 種模仿人類推理的 Action 中選擇一種來執行，生成新的子節點 (新的推理內容)。

我將這 5 個 Action 分為三大類: Linear Reasoning、Decomposition & Refinement、Reformulation。

3.3.1 第一類: Linear Reasoning

這類動作最像標準的 Chain-of-Thought (CoT)，適合處理邏輯比較順暢的部分。

3.3.1.1 Action 1 ($A_1$): Propose a one-step thought

• 做什麼: 根據當前的上下文，只生成「這一步」的推理，而不急著把後面全寫完。
• 為什麼: 這是為了避免 CoT 的「滾雪球錯誤」。標準 CoT 是一口氣寫完，如果中間錯了後面全錯。
• MCTS 視角: 擴展出一個只包含「下一句話」的子節點。

3.3.1.2 Action 2 ($A_2$): Propose the remaining thought steps

• 做什麼: 根據當前狀態，一口氣把剩下的推理步驟全部寫完，直到得出答案。
• 為什麼: 這是為了模擬人類的「快思考」。如果剩下的問題已經變得很簡單了，或者模型很有把握，就不需要一步一步拖泥帶水，直接衝向終點效率更高。
• MCTS 視角: 擴展出一個包含完整後續路徑的子節點 (通常這會直接通向終止節點)。

3.3.2 第二類: Decomposition & Refinement

這類動作專門用來對付複雜、容易出錯的難題，靈感來自 “Least-to-Most Prompting”。

3.3.2.1 Action 3 ($A_3$): Propose next sub-question along with its answer

• 做什麼: 模型不直接解原題，而是問自己: 「為了解決這個大問題，我現在需要先解決哪個小問題？」然後回答這個小問題。
• 為什麼: 複雜問題 (如多步數學題) 直接解容易錯。拆解成小問題 (Sub-questions) 可以降低難度。
• MCTS 視角: 擴展出的節點包含一個「Q: 小問題… A: 小答案…」的結構。

3.3.2.2 Action 4 ($A_4$): Answer the sub-question again

• 限制: 這個動作只能接在 $A_3$ 後面使用。
• 做什麼: 針對 $A_3$ 剛剛提出來的那個子問題，再回答一次。但這次會強制模型使用 Few-shot CoT (思維鏈) 的方式來詳細回答。
• 為什麼: 有時候 $A_3$ 雖然拆解出了對的問題，但回答得太草率或錯了。$A_4$ 就像是一個「檢查機制」或「更認真的解題模式」，確保這個關鍵的子步驟是算對的。
• MCTS 視角: 這是對上一個節點的修正或強化。

3.3.3 第三類: Reformulation

這類動作是為了解決「審題不清」或「鑽牛角尖」的問題。

3.3.3.1 Action 5 ($A_5$): Rephrase the question/sub-question

• 限制: 通常在根節點 (原問題) 或子問題後使用。
• 做什麼: 把題目中的條件重新列點 (List conditions) ，或者換句話說，把題目變得更清晰。
• 為什麼: 很多時候模型做錯是因為忽略了題目中的某個隱藏條件 (比如「正整數」、「不包含」等) 。這個動作模擬人類在卡住時會說: 「等等，讓我重新讀一遍題目，把已知條件列出來…」。
• MCTS 視角: 擴展出的節點不是推理步驟，而是一個「更清晰的題目描述」，後續的推理將基於這個新描述進行。

3.3.4 每次該選擇哪一種 Action?

在像 AlphaGo 這樣的高階系統中，通常會有一個 Policy Network (策略網路) 來預測每個動作的機率 (Prior Probability)。

但在 rStar 這篇論文中，為了保持輕量化並適用於各種 SLM，它並沒有訓練額外的策略網路 (Policy Network) 來決定要選哪一個 Action。相反地，它採用的是「規則限制 (Rule-based Constraints)」搭配 「探索優先 (Exploration First)」的機制。我們可以把它想像成一個帶有規則的清單。

具體來說，決定 Expansion 動作的邏輯分為兩層:

3.3.4.1 第一層過濾: Hard Constraints

並不是這 5 個 Action 在任何時候都能用，必須符合當前的「上下文邏輯」。論文中明確定義了依賴關係 (Dependencies) :

• $A_4$ (Answer sub-question again): 只能在 $A_3$ (Propose sub-question) 之後使用。
  • 邏輯: 你必須先有一個子問題，才能「重新回答」它。
• $A_5$ (Rephrase): 只能在 Root (原始問題) 之後使用 (或者在某些設定下接在子問題後，但主要是針對題目) 。
  • 邏輯: 通常是題目讀不懂或條件複雜時才需要重述。
• $A_1, A_2, A_3$: 這些是比較通用的動作，在大多數推理的中間狀態 (Intermediate States) 都是可用的。

3.3.4.2 第二層決策: UCT 的「未探索優先」機制

這回到了 MCTS 的核心特性。當 Selection 階段選到了一個節點，準備進行 Expansion 時:

• 初始狀態: 所有還沒被嘗試過的 Action (合法的那些) ，它們的訪問次數 $N$ 都是 0。
• 數學結果: 根據 UCT 公式，分母為 0 (或極小) ，這會導致計算出來的數值無限大。
• 決策: MCTS 會強制模型去嘗試那些「還沒試過」的 Action 類型。

換句話說，rStar 採取的策略是「雨露均霑」: 它不會預判哪個動作好，而是傾向於把所有合法的動作類型都試一遍。如果這個節點還沒試過 $A_1$，就做 $A_1$；下次再來如果 $A_1$ 做過了，就試試 $A_3$。

3.3.4.3 補充: 數量限制 (Quota)

為了防止搜索樹無限變寬，論文在 4.1 節 (Implementation Details) 提到了一個很重要的限制:

• $A_1$ (單步) & $A_3$ (子問題): 這兩種動作變化多，允許在同一個節點下最多生成 5 個不同的子節點 (透過採樣不同的內容) 。
• 其他動作 ($A_2, A_4, A_5$): 默認限制為 1 個。

3.3.4.4 總結

所以在 Expansion 階段，決定 Action 的流程是:

1. 列出清單: 根據目前節點的狀態，列出所有合法的 Action 類型 (剔除不符合邏輯順序的) 。
2. 檢查額度: 檢查哪些 Action 類型還沒達到生成數量上限。
3. 隨機/輪詢選擇: 從剩下的合法選項中挑一個 (通常是隨機或依序) ，讓 LLM 去執行生成。

結論: rStar 並不依賴模型去「判斷」當下該用什麼招式最好，而是利用 MCTS 的特性，強迫模型在多次 Rollout 中嘗試各種不同的招式，最後再由 Reward (獎勵機制) 來告訴模型哪一招最有效。

3.4 rStar 中的 “Simulation” 流程

假設現在站在 Child Node (稱之為 $s_1$) 上。這個節點是剛剛透過 Action $A_1$ (Propose a one-step thought) 生成的，所以它目前只包含「第一步」的推理內容 (例如:「Step 1: 先計算原本有多少顆蘋果…」)，還沒有最終答案。

如果我們停在這裡，根本不知道這一步寫得好不好。Simulation (又稱 Rollout) 的目的，就是透過「快速預演未來」，來評估這個節點 ($s_1$) 究竟能不能通往正確的結局。

以下是 rStar 論文中 Simulation 階段的詳細步驟:

3.4.1 Default Policy Rollout

在這個階段，MCTS 會切換成一個比較簡單、快速的模式 (Default Policy)。

• 輸入: 題目 + 目前節點 $s_1$ 的內容。
• 指令: 告訴 LLM:「請根據已經寫好的 Step 1，把剩下的推理步驟全部補完，直到算出答案。」
• 動作: 這時候通常不使用那些複雜的 $A_3, A_4, A_5$ 動作，而是類似於 Action $A_2$ (Propose remaining steps) 的邏輯，讓模型一口氣生成到底。

3.4.2 Terminal State

LLM 執行完上述指令後，會生成一條完整的軌跡 (Full Trajectory):

這時候我們拿到了一個最終答案 (例如:「答案是 42」)。

3.4.3 Reward Calculation —— 關鍵的評分標準

現在我們手上有了最終答案，要怎麼給 $s_1$ 打分 (計算 $Q$ 值) 呢？

這篇論文遇到了一個大挑戰: 這是推理任務 (Inference)，沒有標準答案 (Ground Truth) 可以對照。 因此，rStar 採用的方法是 Self-Consistency Majority Voting Estimation。

在論文的 4.1 Experiment Setup 中的 Implementation Details 中，有提到 “In the trajectory self-generation stage, we augment each target SLM with our MCTS, performing 32 rollouts.” 這裡的意思是 MCTS 的 4 階段流程 (Selection -> Expansion -> Simulation -> Backpropagation) 會進行 32 次，每次都會得到一個完整的軌跡 (Full Trajectory) 以及最終答案，因此總共會得到 32 個完整的軌跡 (Full Trajectory) 以及最終答案。

因此，在 rStar 中會將每次 Simulation 得到的最終答案與 MCTS 目前答案池中的答案 (最多 32 個) 進行比較來計算 Reward:

1. Answer Pool: 在整棵 MCTS 樹的搜索過程中，我們會生成很多條路徑，得到很多個答案。
2. Self-Consistency Majority Voting: 我們會看哪個答案出現最多次。假設「42」在所有嘗試中出現頻率最高，我們就暫時認為「42」是正確答案。
3. Reward:
   • 如果這次 Simulation 算出來的答案是「42」(和主流意見一致)，這次模擬就得到 高分 (Reward = 1)。
   • 如果算出來是「15」(非主流意見)，就得到 低分 (Reward = 0)。

在 MCTS 的初期 (剛開始跑前幾輪)，答案池還很小，這個評分可能不太準。但隨著 Rollout 次數增加 (論文設定是 32 輪)，「正確答案」通常會因機率優勢而浮現，評分就會越來越準。

3.5 rStar 中的 “Backpropagation” 流程

如果說 Selection 是「決策」，Expansion 是「行動」，Simulation 是「評估」，那麼 Backpropagation 就是 「學習與歸納」。這是 MCTS 真正變聰明的關鍵時刻。

在 rStar 這篇論文中，Backpropagation 的實作非常直觀，但有一個為了適應 SLM (小模型) 而做的關鍵設計選擇。

我將其拆解為三個部分來說明:

3.5.1 核心任務: 更新什麼？

當 Simulation 結束，我們得到了一個 Reward (記為 $R$)。現在，我們要沿著剛剛走過來的路徑 (從當前的 Leaf Node 一路回到 Root Node)，更新路徑上每一個節點的兩個統計數據:

1. $N(s, a)$ (訪問次數 Visited Count):
   • 告訴這個節點:「嘿，我們又經過你一次了！」
   • 更新方式:$N \leftarrow N + 1$
2. $Q(s, a)$ (累積價值 Total Reward Value):
   • 告訴這個節點:「這次經過你之後，我們拿到了一個 $R$ 分的結果，把它記在帳上！」
   • 更新方式:$Q \leftarrow Q + R$

3.5.2 rStar 的關鍵設計: 只看結果，不問過程 (Outcome-based Reward)

這是這篇論文的一個重點。許多進階的 MCTS 方法 (例如 AlphaGo) 或者其他的 Reasoning 方法 (如 RAP)，會試圖給中間的每一個步驟打分 (Intermediate Reward)。

但在 rStar 中，作者特意避開了給中間步驟打分。

• 為什麼？ 因為 SLM 能力較弱，讓它自己評估「這一步推理好不好」(Self-rewarding) 通常評不準，甚至跟隨機猜差不多 (論文 Appendix 有證明這一點)。
• 怎麼做？ rStar 採用 Sparse Reward (稀疏獎勵) 的策略。
  • 中間節點本身的「內在價值」設為 0。
  • 它們的價值完全取決於最終 Simulation 跑出來的那個結果。

具體操作流程:

假設我們這次生成的路徑是: Root (題目) $\rightarrow$ Node A (第一步) $\rightarrow$ Node B (第二步) $\rightarrow$ [Simulation] $\rightarrow$ 最終答案

假設 Simulation 根據多數決給出的 Reward $R = 0.8$。

Backpropagation 更新過程:

1. 更新 Node B:
   • $N_B \leftarrow N_B + 1$
   • $Q_B \leftarrow Q_B + 0.8$
2. 更新 Node A:
   • $N_A \leftarrow N_A + 1$
   • $Q_A \leftarrow Q_A + 0.8$
3. 更新 Root:
   • $N_{root} \leftarrow N_{root} + 1$
   • $Q_{root} \leftarrow Q_{root} + 0.8$

意義: 這意味著 Node A 和 Node B 對於這個「好結果」有同等的功勞。這是一種簡化但有效的歸因方式 (Credit Assignment)。

3.5.3 與 UCT 公式的連動

這一步更新完畢後，整棵樹的數據就變了。

• 因為 $N$ 變大了，這條路徑上的節點在下一次 Selection 階段的 Exploration (探索項) 數值會變小(分母變大)。
• 因為 $Q$ 變大了(假設 $R$ 是正的)，這條路徑的 Exploitation (利用項，即平均勝率 $Q/N$) 可能會變高。

這就形成了一個閉環:

• 如果這次結果好 ($R=1.0$) $\rightarrow$ $Q$ 大幅增加 $\rightarrow$ 平均分提高 $\rightarrow$ 下次更容易被選中 (Exploitation)。
• 如果這次結果差 ($R=0.0$) $\rightarrow$ $Q$ 不變但 $N$ 增加 $\rightarrow$ 平均分被拉低 $\rightarrow$ 下次可能會嘗試別的路 (Exploration)。

3.6 rStar 中的 Mutual Reasoning for Final Answer

做完了 32 次 Rollout (Selection -> Expansion -> Simulation -> Backpropagation)，我們目前得到了 32 個完整的軌跡 (Full Trajectory) 以及最終答案。接下來的問題是: 怎麼決定最終答案?

所以，rStar 引入了第二階段:Mutual Reasoning 與 Discriminator。這 32 條 Trajectory 會經過一個「嚴格的過濾與驗證」流程，具體步驟如下:

3.6.1 Discriminator

• 是誰？ 另一個能力相當的小模型 (SLM)，或者甚至是同一個模型扮演不同角色。
• 任務: 它的工作不是直接給這 32 條路徑打分 (比如「這題給 80 分」)，因為小模型通常評分不準。
• 方法: 它的工作是 「填空測試」。

3.6.2 Mask-and-Complete

對於這 32 條 Trajectory 中的每一條(我們稱之為 $t$)，系統會進行以下操作:

1. Masking:

   • 假設某一條 Trajectory $t$ 總共有 5 個步驟 ($s_1, s_2, s_3, s_4, s_5$)。
   • 系統會隨機選一個切割點 (論文提到是隨機保留前 20% 到 80% 的步驟)。
   • 比如保留前 3 步 ($s_1, s_2, s_3$)，把後面的 ($s_4, s_5$) 遮住 (Mask 掉)。

2. Completion:

   • 把題目和保留的前半段 ($s_1, s_2, s_3$) 丟給 Discriminator。
   • 指令:「請根據前面的步驟，把剩下的推理步驟補完，並算出答案。」
   • Discriminator 會生成一個新的結尾和新的答案(記為 $\hat{A}$)。

3.6.3 Mutual Consistency Check

現在我們有兩個答案:

• 原版答案 ($A$): 來自 Generator 生成的那條完整 Trajectory。
• 重寫版答案 ($\hat{A}$): 來自 Discriminator 根據前半段補完的結果。

判斷標準:

• 如果 $A == \hat{A}$: 恭喜！這條路徑被視為 Mutually Consistent。這代表這條路徑的邏輯很穩健，連另一個模型看到一半都能推導出同樣的結果。這條路徑的可信度大大提升。
• 如果 $A \neq \hat{A}$: 警報！這條路徑可能存在邏輯跳躍或運氣成分，導致另一個模型接不下去或接出了不同的結果。

3.6.4 Final Selection

透過 Mutual Reasoning 與 Discriminator，我們可以把 Generator 產生的 32 條 Trajectory 進行篩選。基於剩下的 Trajectory，我們要挑出唯一的「王者」作為最終回答。

我們會透過以下公式計算剩下的 Trajectory 的分數，然後挑選出分數最高的作為最終答案:

3.6.4.1 MCTS Reward

• 來源: 這是來自 MCTS 搜索樹 (Generator) 的數據。
• 具體指什麼: 指的是該條 Trajectory 對應的終端節點(Terminal Node)在 MCTS 中的 $Q$ 值(或者說是經過標準化後的 $Q$ 值)。
• 代表意義: 「這條特定的推理路徑(Path)品質如何？」
  • 在 MCTS 的過程中，如果這條路徑($t$)被訪問過多次，且每次都能導向高分答案，它的 $Q$ 值就會很高。
  • 這代表 Generator 認為:「按照這個步驟走，邏輯是很順暢、很穩的。」

3.6.4.2 Confidence Score

• 來源: 這是來自 32 次 Rollouts 的答案池 (Answer Pool) 的統計數據。
• 具體指什麼: 指的是這條路徑最終得出的「那個答案」，在所有 32 次嘗試中出現的頻率 (即 Self-Consistency Majority Voting 的機率)。
• 代表意義: 「這個最終答案 (Answer) 的可信度如何？」
  • 這與路徑無關，只看結果。
  • 例如:如果 32 次裡面有 28 次都算出 “42”，那 “42” 的 Confidence Score 就是 $28/32 = 0.875$。

3.6.4.3 為什麼要相乘?

假設我們現在有兩條通過了 Discriminator 驗證的 Trajectory (稱為 A 和 B)，它們都算出了正確答案 “42”。我們該選哪一條作為最終輸出的「詳解」?

• Trajectory A:

  • 是一條很常見、很穩健的路徑 (MCTS 經常走到這裡)。
  • $Q$ 值 (Reward) = 0.9 (路徑品質高)
  • 答案 “42” 的 Confidence = 0.875 (答案很熱門)
  • Final Score = $0.9 \times 0.875 = \mathbf{0.7875}$

• Trajectory B:

  • 是一條比較冷門的路徑 (MCTS 很少走到，或者偶爾會導致錯誤)，但這次剛好算對了，也通過了 Discriminator 驗證。
  • $Q$ 值 (Reward) = 0.4 (路徑品質低，可能是賽到的)
  • 答案 “42” 的 Confidence = 0.875 (答案依然很熱門)
  • Final Score = $0.4 \times 0.875 = \mathbf{0.35}$

通過相乘，系統會傾向於選擇 「既能導出高共識答案 (Confidence 高)，其推理過程本身也被 MCTS 驗證為高品質 (Reward 高)」 的那條 Trajectory。這避免了選到那種「雖然答案對了，但過程是歪打正著」的路徑，確保輸出給用戶的解題步驟是最標準、最穩健的。

4 rStar 的實驗結果

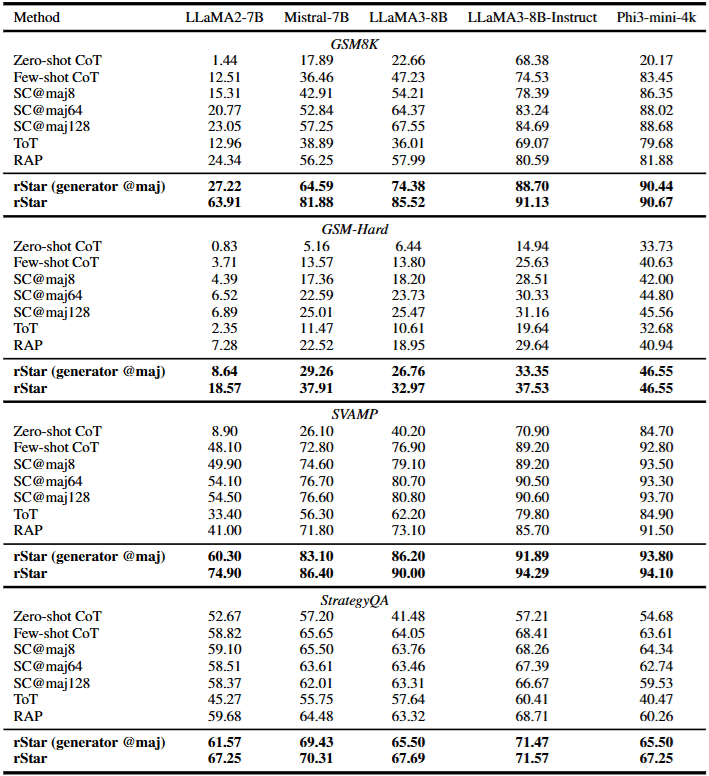
rStar (generator @maj) 表示單純根據 Generator 所進行的 32 次 Rollout，透過 Majority Voting 決定 Final Answer (完全沒有使使用到 Discriminator)。

從上表中可以發現到，即使在完全沒有使用 Discriminator 做 Mutual Reasoning 的情況下，rStar 的表現仍然比 Baseline 方法好，說明 rStar 中的所設計的 Generator 是有效的。如果加上 Discriminator 做 Mutual Reasoning，最終表現又會顯著提升。

在閱讀上表的實驗數據時，我產生了一個問題:

單純的 SC(Self-Consistency)@maj64 其實就達到很不錯的表現，如果 rStar 針對一個 Task 所需要的平均 LLM Call 遠高於 64 次，然後表現又沒有比 SC@maj64 提升更多的話，那這個方法是不是效益沒有那麼大?

實際上，論文在 Appendix A.2 的 Table 7 中非常誠實地列出了這個數據。

• 具體的 LLM Call 次數，根據論文數據 (以 GSM8K 為例):
• LLaMA2-7B: 平均需要 166.81 次 calls。
• Mistral-7B: 平均需要 148.90 次 calls。

這 ~150-160 次 LLM Call 是怎麼來的?

1. Generator (MCTS): 為了生成 32 條完整的 Trajectories，MCTS 雖然只做 32 次 Rollout，但因為中間有 Expansion (生成 Action)和 Simulation (補完路徑)，且樹的結構有分支，平均大約消耗 120-130 次 calls。
2. Discriminator: 針對生成的 32 條路徑進行驗證，固定需要 32 次 calls。
3. 總計: $120 + 32 \approx 150+$ 次。

rStar 的成本大約是 SC@64 的 2.3 ~ 2.6 倍 (接近 SC@128 或 SC@192 的等級)。

除了 LLM Call 的次數，論文還提到了一個更驚人的數字:Generated Tokens。

• rStar 平均每題會生成 36 萬 (367.1k) 個 Tokens。
• 這是因為 MCTS 的每一條路徑往往都很長 (包含多步推理、子問題拆解)，加上 Discriminator 也要讀很長的 Context。

相比之下，SC@64 如果每條路徑 200 tokens，總共也才 1.28 萬 tokens。rStar 的 Token 成本大約是 SC@64 的 20~30 倍。

但是，我們必須看 「投資報酬率 (ROI)」，也就是增加這些成本換來了多少準確率提升。這取決於模型的基礎能力。

• 情境 A:弱模型 (Weak SLMs) —— rStar 完勝 (以 LLaMA2-7B 為例 (看 Table 2)):
  • SC@64: 準確率 20.77%
  • SC@128: 準確率 23.05% (即使加倍到 128 次，提升也非常微弱)
  • rStar (~160 calls): 準確率 63.91%

結論: 在這種情況下，rStar 的效益是巨大的。 為什麼？因為弱模型有嚴重的「系統性錯誤」。SC@64 只是讓它把錯誤的邏輯重複 64 次 (Garbage In, Garbage Out)。rStar 透過 MCTS 的 Action 引導，硬是把模型的能力邊界推了出去，解決了 SC 堆數量也解決不了的問題。這裡的成本增加是非常值得的。

• 情境 B:強模型 (Stronger SLMs) —— 差距縮小 (以 LLaMA3-8B-Instruct 為例)
  • SC@64: 準確率 83.24%
  • rStar: 準確率 91.13%

結論: 提升了約 8%。 這時候就要看應用場景了。如果你追求極致的準確率(從 83 分考到 91 分)，這 2.5 倍的成本是可以接受的。但如果你資源有限，SC@64 已經夠好了。

rStar 方法與 Self-Concsistency 方法選擇的總結:

1. 解決「不會做」的問題: rStar 真正的價值在於「雪中送炭」。當模型本身能力不足(如 LLaMA2-7B 面對數學題)，SC 採樣再多次都沒用，這時 rStar 能讓模型「變聰明」，這是 SC 做不到的。
2. 解決「粗心」的問題: 當模型已經很強(如 GPT-4 或 LLaMA3)，只是偶爾粗心，SC (Self-Consistency) 的 CP 值通常更高。
3. 結論: rStar 的效益在於挖掘 SLM 的潛力上限，而不是單純為了省錢。如果你的任務是 SLM 覺得很難的(準確率低於 50%)，rStar 是非常強大的工具；如果任務對模型來說很簡單，用 SC 就夠了。

這是目前 AI 領域非常熱門的話題:Weak-to-Strong Generalization。 我們之前討論過 Discriminator(判別器)的角色。我們可能會直覺認為:「要檢查 LLaMA3-8B 的答案，判別器至少也要是同等級的吧？」

但在上表中，作者做了一個有趣的實驗:

• Generator: LLaMA3-8B-Instruct
• Discriminator: 換用不同等級的模型。

結果令人驚訝:

• 用 Phi-3-Mini (3.8B) 當判別器:準確率 91.13%
• 用 GPT-4 (超強模型) 當判別器:準確率 92.57%

解讀: 這說明了 rStar 的 Mutual Consistency 機制非常強大。即使是一個比 Generator 弱很多的 Discriminator (3.8B vs 8B)，只要它能進行基本的邏輯補全，就能有效地篩選出正確答案。這對於降低部署成本來說是個巨大的好消息(你可以用一個小模型來監控大模型)。

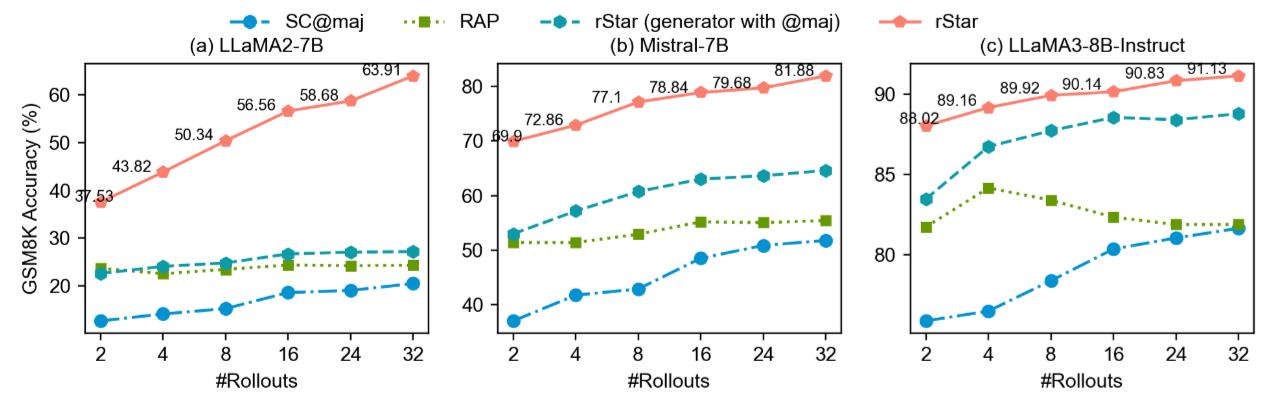
剛剛我們討論到 rStar 的成本很高 (32 rollouts)。但如果我們看上表，會發現一個很棒的趨勢。

現象:

• 當 Rollout 次數只有 2 次 (2 Rollouts) 時，rStar 的表現就已經顯著超越了其他的 Baseline (如 RAP 和 SC)。
• 曲線在 8~16 次 Rollout 時就已經趨於飽和，後面的提升幅度變小。

這回應了我們剛才對成本的擔憂。雖然論文設定是 32 次，但在實際應用中，我們其實可以把 Rollout 砍到 4 次或 8 次。這樣 LLM Call 的次數會大幅下降 (可能只比 SC 多一點點)，但依然能享受到 MCTS 帶來的結構化推理優勢。這證明了 rStar 生成的高質量路徑 (High-quality Trajectories)在非常早期就能被找到。

我們花了很多時間討論那 5 個 Action ($A_1 \sim A_5$)。你可能會問:「真的需要搞這麼複雜嗎？只用一招不行嗎？」

上表給出了答案(以 LLaMA3-8B 為例):

• 只用 $A_3$ (像 RAP 方法): 70.5%
• 只用 $A_3 + A_5$: 72.5%
• 全部用 ($A_1 \sim A_5$): 75.0%

這證明了 “Rich set of human-like reasoning actions” 的價值。單一的拆解策略(如 RAP)雖然有用，但在面對多樣化的題目時不夠靈活。多加入「重述問題 ($A_5$)」和「單步/多步切換 ($A_1/A_2$)」，確實能覆蓋更多類型的推理盲點。這也提醒我們，未來的研究方向可以是設計更多樣化的推理動作。

5 結語

最後總結本篇論文三個最重要的核心觀念:

1. Inference Scaling Laws: 這篇論文證明了，除了在訓練端 (Pre-training/Fine-tuning) 堆算力，我們也可以在**推理端(Inference-time)**堆算力 (透過 Search 和 Verification) 來大幅提升模型能力。這是不需要重訓模型就能變強的路徑。
2. Mutual Reasoning: 「自我驗證」很難，但「互助驗證」(填空題測試) 很有效。這種透過一致性 (Consistency) 而非直接評分 (Scoring) 的驗證方法，是解決 Reward Model 難訓練的一個巧妙解法。
3. MCTS as a Prompting Driver: 傳統 MCTS 用於下棋，rStar 把它變成了 Prompt 的調度器。這展示了將經典算法 (Classic Algo) 與 LLM 結合的強大潛力。