RLHF 讓模型變無聊？揭秘「典型性偏差」與 Verbalized Sampling 如何喚醒 LLM 潛在的創造力

1 前言

在當前的 AI 研究中，我們經常發現一個令人沮喪的現象: 經過精細對齊 (Alignment，如 RLHF 或 DPO) 的模型，雖然變得更安全、更聽話，但也變得「更無聊」了。它們的創造力似乎被閹割，輸出往往千篇一律。這篇論文 Verbalized Sampling: How to Mitigate Mode Collapse and Unlock LLM Diversity 提供了一個全新的視角。

不同於過去將問題歸咎於算法缺陷，這篇論文指出問題的根源在於數據——具體來說，是人類偏好數據中的**典型性偏差 (Typicality Bias) **。為了克服這個問題，作者提出了一種無需訓練 (Training-free) 的推理策略: Verbalized Sampling (VS)。

在這篇文章中，我們將一步步重現論文的推導過程，理解為什麼模型會「坍縮」，以及如何透過簡單的 Prompting 技巧「喚醒」模型被壓抑的多樣性。

2 問題定義: 為什麼模型的多樣性會下降？

2.1 核心現象: 模式坍縮 (Mode Collapse)

首先，我們需要定義什麼是 Mode Collapse。 經過後訓練 (Post-training) 的模型，其輸出的概率分佈會變得極度尖銳 (Sharpened) 。這導致模型傾向於反覆輸出極少數的「安全牌」或「標準答案」，即分佈中的 **Mode (眾數/模式) **。

2.2 理論歸因: 典型性偏差 (Typicality Bias)

論文提出了一個大膽的假設: 人類有一種天生的認知偏差，傾向於給那些「看起來很熟悉」、「符合直覺」的文本更高的分數。

人類的這樣天生的 Bias 會反映在我們所建立的 Preference Dataset 上，使得基於此 Dataset 訓練出來 Reward Model 也會有這樣的 Bias，進而使得基於此 Reward Model 進行後訓練的語言模型，也學習到這樣的 Bias。

為了量化這一點，作者建立了 Reward Model 的數學模型:

• $r(x, y)$: 人類給出的總獎勵。
• $r_{\text{true}}(x, y)$: 真實的任務的客觀評分 (例如：正確性、是否有符合指令) 。
• $\log \pi_{\text{ref}}(y \mid x)$: 預訓練模型 (Base Model) 的 Log-Likelihood。
• $\alpha$: 典型性偏差係數。

為什麼作者使用 Base Model ($\pi_{\text{ref}}$) 來代表典型性？

這基於作者的一個重要的假設: 預訓練模型 (Base Model) 是在海量的人類文本上進行訓練的，因此它捕捉了人類語言的統計規律與分佈。 換句話說，如果一個句子在 Base Model 中的機率很高 (High Log-likelihood) ，就代表這個句子非常符合人類的日常用語習慣、非常「典型」。因此，作者將 Base Model 的 Log-likelihood 作為人類心中「熟悉感」與「典型性」的最佳數學代理 (Proxy) 。

2.2.1 驗證 $\alpha > 0$: 控制變量實驗

為了證明 $\alpha$ 真的存在，作者利用了 HelpSteer 數據集進行實驗。實驗設計非常精妙:

1. 挑選出 Correctness (正確性) 相同 的 Response Pair。這意味著消除了 $r_{\text{true}}$ 的影響。
2. 觀察這兩者中，人類更傾向於認為哪個 Helpful (有用)。
3. 使用 Bradley-Terry Model 進行回歸分析，估計 $\alpha$。

實驗結果顯示 $\alpha \approx 0.6$，證實了人類所標註的 Preference Dataset 中確實顯著偏好典型內容，而我們現在的 Reward Model 也會學習到這樣的 Bias。

2.3 數學證明: 偏差如何導致坍縮

知道了 $\alpha > 0$，這如何導致 Mode Collapse 呢？讓我們一步步推導。

2.3.1 RLHF 的優化目標

RLHF 的目標是在最大化 Reward 的同時，限制與 Base Model 的 KL 散度，以防止模型崩壞:

其中 $\beta$ 是 KL 懲罰係數。

2.3.2 Closed-Form Solution

根據強化學習理論，上述目標函數的最佳解 $\pi^*$ 具有以下 Closed-Form Solution:

2.3.3 代入帶有偏差的 Reward 函數

現在，我們將前面驗證過的偏差 Reward 函數 $r(x, y) = r_{\text{true}} + \alpha \log \pi_{\text{ref}}$ 代入上式:

2.3.4 利用對數律進行合併

利用數學性質 $e^{k \log x} = x^k$，我們可以將最後一項轉換: $\exp\left( \frac{\alpha}{\beta} \log \pi_{\text{ref}} \right) = \pi_{\text{ref}}^{\frac{\alpha}{\beta}}$。

接著將所有的 $\pi_{\text{ref}}$ 合併:

2.3.5 定義 $\gamma$ 與結論

我們定義縮放係數 $\gamma = 1 + \frac{\alpha}{\beta}$，最終得到:

2.3.6 關鍵結論

由於 $\alpha > 0$ (典型性偏差存在) 且 $\beta > 0$，因此 $\gamma > 1$。 這意味著我們對 Base Model 的概率分佈取了一個大於 1 的冪次。數學上，這會導致強者越強，弱者越弱 (例如 $0.9^2=0.81$, $0.1^2=0.01$，差距被拉大了) 。

這就是 Mode Collapse 的數學本質: 分佈被極度「銳化」 (Sharpening) ，導致模型被迫坍縮到機率最高的那個 Mode 上。

3 方法介紹: Verbalized Sampling (VS)

既然問題出在 RLHF 後的分佈太尖了，我們能不能讓模型自己把這個分佈「還原」回來？作者提出了 Verbalized Sampling。

3.1 核心洞察: 不同的 Prompt 坍縮到不同的 Mode

作者將 Prompting 分為三個層次:

1. Instance-level (傳統問法): “Tell me a joke.” -> 模型直接採樣，受制於 $\gamma$，只會輸出最常見的那個笑話。
2. List-level (列表問法): “Tell me 5 jokes.” -> 模型進行序列生成。由於它依然是在貪婪地尋找高分區，且隱含了均勻分佈假設，它往往只會列出 5 個非常相似的變體。這無法解決 Mode Collapse。
3. Distribution-level (VS): “Generate 5 jokes and their probabilities.” -> 這是本篇的核心。

3.2 核心機制: Verbalize Probabilities

當我們要求模型 「口頭說出機率」 時，模型的任務從「採樣 (Sampling) 」變成了「描述 (Describing) 」。

• 模型被迫調用底層的知識來估計分佈，這能有效繞過 RLHF 的銳化效應。
• 理論證明 (見論文 Appendix) 顯示，這種方式重構出的分佈，能高度逼近預訓練階段 (Pre-training) 的原始分佈。

以下是三種主要的 VS Prompt 寫法:

3.2.1 VS-Standard (標準版)

最通用、最基礎的版本，適用於大多數任務。

You are a helpful assistant.

Instruction:
Generate 5 responses to the input prompt: "{input_prompt}"

Format Requirements:
Return the responses in JSON format with the key: "responses" (a list of dictionaries). Each dictionary must include:
1. "text": the response string itself.
2. "probability": the estimated probability of this response (from 0.0 to 1.0) given the input prompt, relative to the full distribution of possible responses.

Input Prompt:
{input_prompt}

3.2.2 VS-CoT (思維鏈版)

結合 Chain-of-Thought，讓模型先思考多樣性策略，再生成分佈。適合複雜寫作任務。

Instruction:
Generate 5 responses to the input prompt using chain-of-thought reasoning.

Step 1:
Provide a "reasoning" field. Analyze the request and think about different angles, styles, or perspectives to ensure diversity in the responses.

Step 2:
Generate the responses in JSON format with the key "responses". Each item must include:
- "text": the response string.
- "probability": the estimated probability relative to the full distribution.

Input Prompt:
{input_prompt}

3.2.3 VS-Multi (多輪對話版)

透過多輪對話挖掘長尾分佈。第一輪生成後，將結果放入歷史，第二輪要求生成「不同」的內容。

System:
(Keep previous context)

User:
Generate 5 MORE alternative responses to the original input prompt. These should be distinct from the previous ones.

Format Requirements:
Return the responses in JSON format with the key "responses", including "text" and "probability" (relative to the full distribution).

4 實驗結果

我們關注四組關鍵實驗數據，來驗證 VS 的有效性。

4.1 多樣性與質量的權衡 (Diversity-Quality Trade-off)

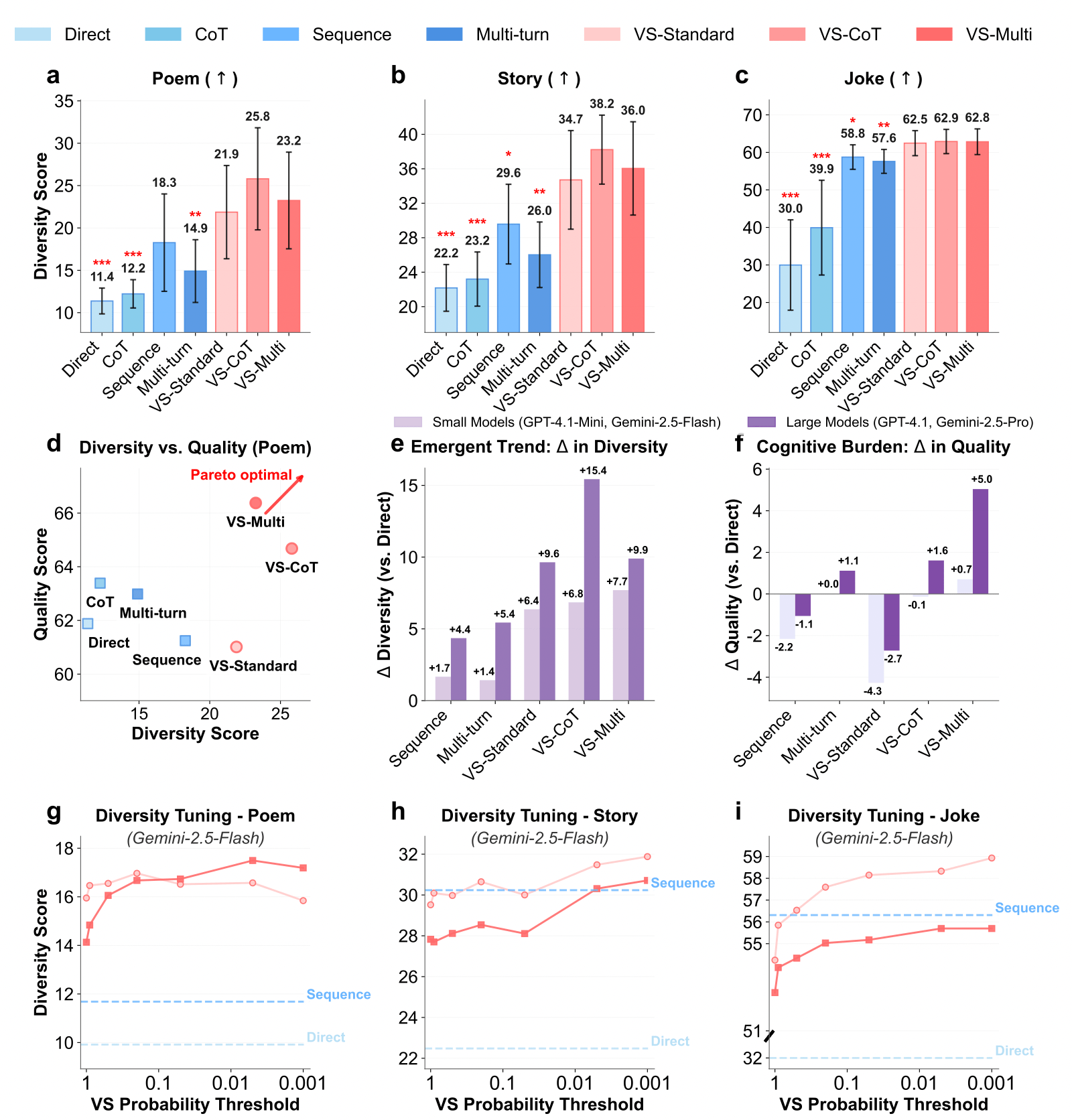
• Pareto Front: 在 Figure 4(d) 中，VS-CoT（紅線）將整條曲線向右上方推移。這意味著在相同的質量下，VS 提供了更高的多樣性。
• 人類評估: 在 Joke 任務中，VS 的多樣性評分（3.01）顯著高於直接問法（1.83）。
• 湧現趨勢 (Emergent Trend): 如 Figure 4(e) 所示，越強的模型（如 GPT-4.1）使用 VS 獲得的多樣性增益（Diversity Gain）遠大於小模型（如 GPT-4.1-mini），證明此方法依賴模型的指令遵循與校準能力。

4.2 理論驗證：預訓練分佈的還原

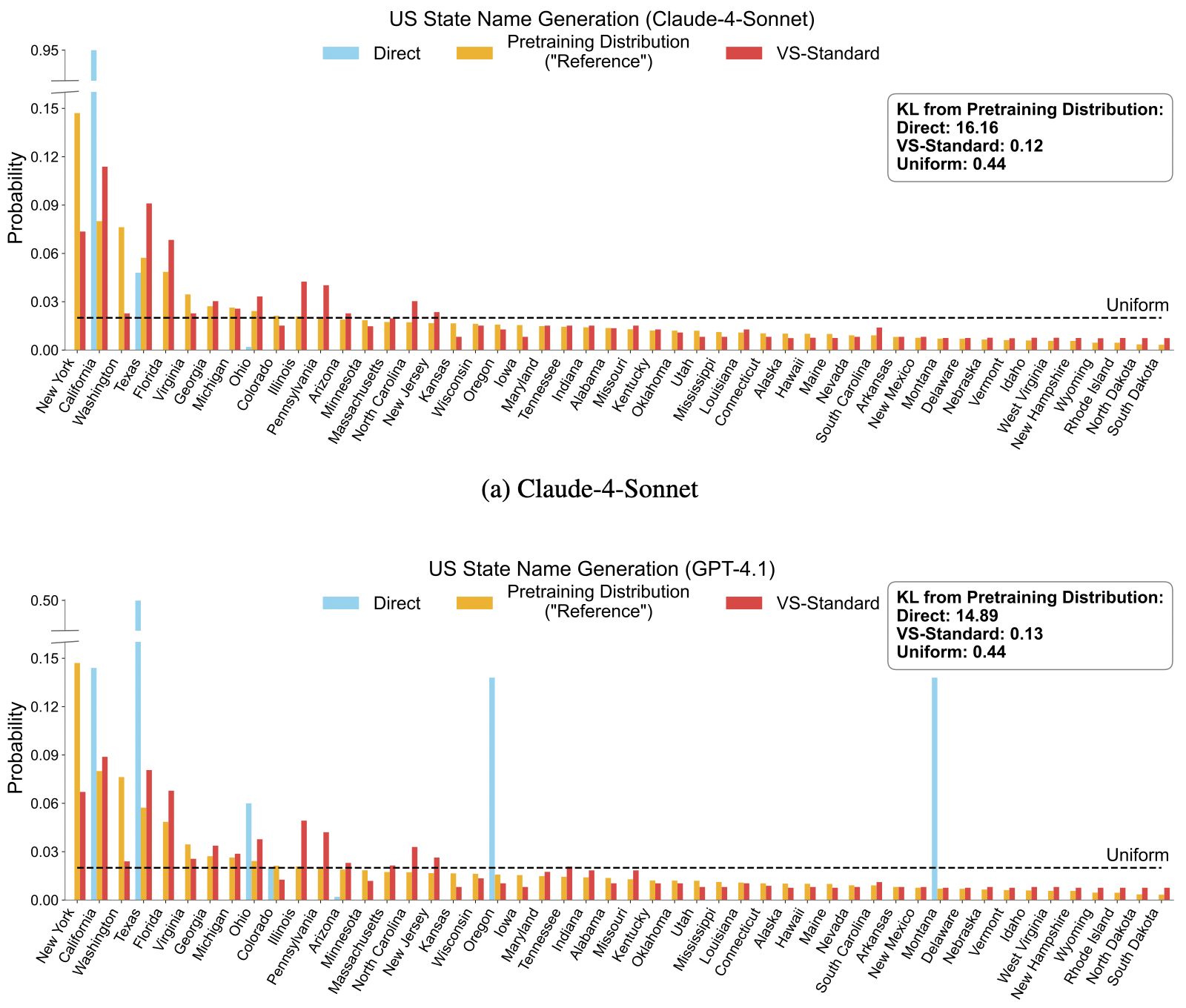
在 “Name a US State” 的實驗中，作者計算了生成分佈與真實預訓練數據分佈的 KL Divergence。

• Direct Prompting: KL $\approx 14.8$ (嚴重坍縮)
• VS-Standard: KL $\approx 0.13$ (幾乎完美還原) 這直接證實了 VS 能成功喚醒模型被壓抑的知識分佈。

4.3 下游任務應用：合成數據生成

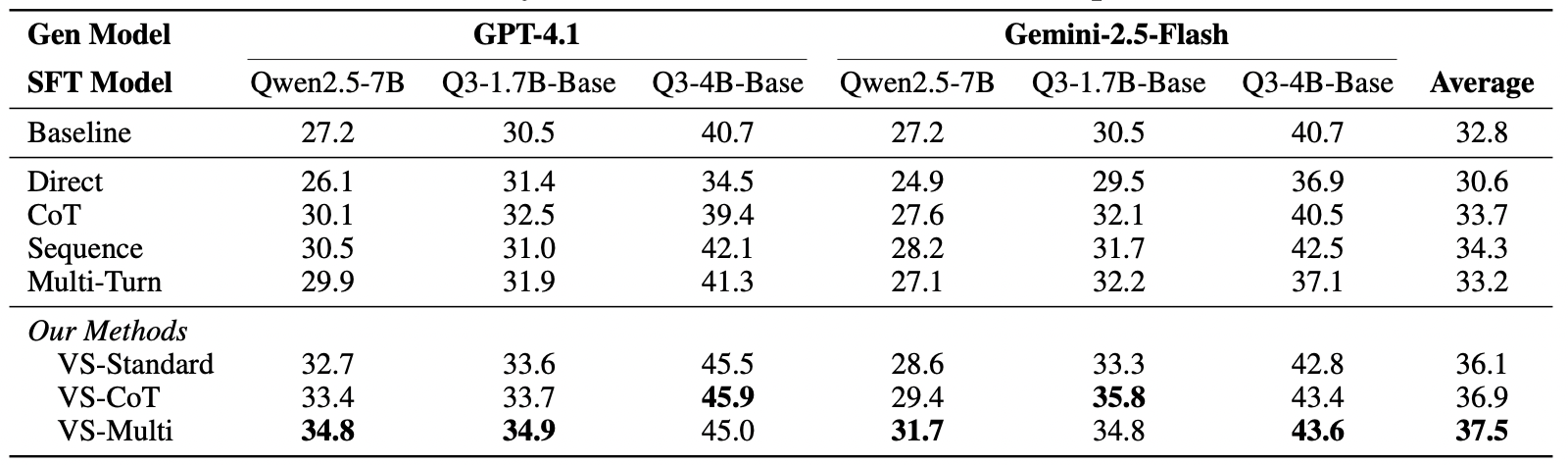
VS 不僅能寫詩，還能提升數學能力。

• 實驗設計：使用 VS 生成數學題目來微調小模型。
• 結果顯示，相比 Baseline (30.6%)，使用 VS-Multi 生成的數據微調後，準確率提升至 37.5%。這證明了 VS 生成的數據具備高質量與高覆蓋率，對於 Data Synthesis 領域極具價值。

5 結論

這篇論文帶給我們最重要的啟示是：模型的「平庸」與「缺乏創意」，往往不是因為它沒能力，而是因為它太想討好人類的「典型性偏好」。

透過 Verbalized Sampling，我們不需要昂貴的重新訓練，只需要改變我們與模型溝通的方式——從單純的「索取答案」轉變為「探討可能性」——就能解鎖 LLM 深層的創造力潛能。這為未來的推理加速、數據合成以及創意輔助工具提供了一個極具潛力的方向。